目录
General Mathematics
Existence proof
One kind of the importance theorem in mathematics is the existence theorem which states something with certain property exists. Basically, there are two kinds of proof of the existence theorem.
- Construction. E.g. existence of smooth but not differentiable function.
- Proof by contradiction. E.g. infiniteness of prime numbers, Brouwer fixed point theorem.
Flavors of mathematics
I want to quote the word of Charles Fefferman to show my flavors of mathematics.
Mathematics at the highest level has several flavors. On seeing it, one might say
- What amazing technical power!
- What a grand synthesis!
- How could anyone not have seen this before?
- Where on earth did this come from?
In my opinion, the proof of Fermat’s last theorem by Wiles of kind 1; Langlands conjecutre is of kind 2; the mirror symmetry conjecture or its computation on Calabi-Yau quintics is of kind 3; Tao and Green’s proof of the primes contain arbitrarily long arithmetic progressions of kind 4.
Some advices
From Vakil’s page on advice for listening to talks.
- a definition you want to remember (e.g. “a K3 surface is…")
- a theorem you want to remember (“the moduli space of polarized K3 surfaces is smooth”)
- a motivating or key example (“a quartic is an example of a K3 surface”)
- a motivating problem (“why are all moduli spaces of polarized K3 surfaces the same dimension?")
- a question you want to ask the speaker (“why is that hypothesis in your theorem?")
- a question you want to ask someone else (a definition, motivation, a question about a connection etc.)
- anything else of a similar flavor: something specific that made you think. Something vague (“I liked the part where she talked about groups”) does not count as a “thing”.
From Kedlaya’s page, One important point to keep in mind is that unlike at earlier stages in one’s education, in graduate school and beyond one very often learns mathematics “in reverse”. That is, it is often necessary to work through a particular piece of mathematics before one is familiar with its logical prerequisites; the switch from forward to reverse study of mathematics is quite a difficult transition (at least according to my own experience as a student).
Category Theory
TODO A_∞ algebra
TODO A_∞ category
Abelian
A category is abelian if it is Exact and Additive.
Additive
A category \(\mathcal{C}\) is called additive if the following conditions hold.
- For any two object \(\Hom(X,Y)\) has an abelian group structure and compositions are bilinear.
- There is a zero object, denoted by \(0_{\mathcal{C}}\).
- For any two objects \(X, Y\), the direct sum \(X \oplus Y\) exists in \(\mathcal{C}\).
A functor is called additive if it induces group homomorphism on homomorphisms.
Adjoint
Let \(F: \mathcal{C} \to \mathcal{D}\) and \(G: \mathcal{D} \to \mathcal{C}\) two functors. We say that \(G\) is right adjoint to \(F\) and \(F\) is left adjoint to \(G\) if there is an isomorphism \[\Hom_{\mathcal{D}}(F(X), Y) \cong \Hom_{\mathcal{C}}(X, G(Y))\]
Anodyne extension
Anodyne extensions denote the class of morphisms \(\Lambda_{k}^{n} \subset \Delta^{n}\).
Referenced: Kan fibration.
Associativity constraint
For \(\mathscr{C}\) category with functor \(\otimes\), an associativity constraint is a functorial isomorphism \[\phi: X \otimes (Y \otimes Z) \to (X \otimes Y) \otimes Z\] satisfying pentagon identity.
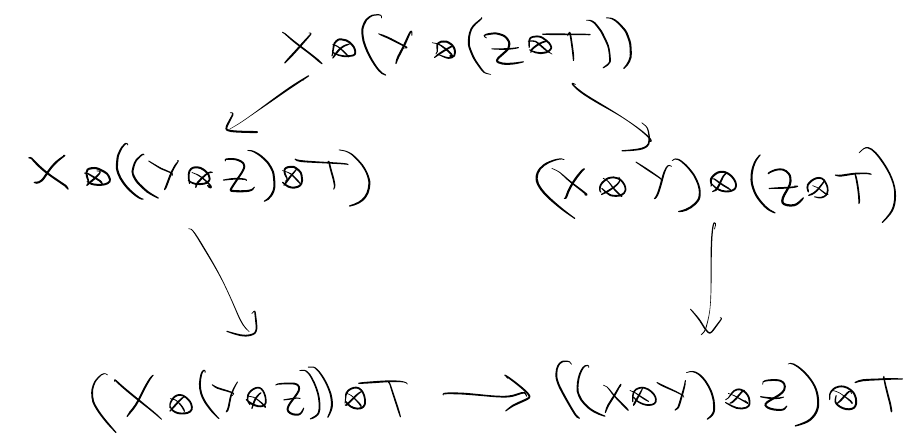
Referenced: Monoidal category, Tensor category, Rigid, Tensor functor.
TODO Bialgebra
Category
A category \(\mathcal{C}\) consists of the following data
- A collection of objects.
- For every pair of objects \(X, Y \in \mathcal{C}\), a set \(\Hom_{\mathcal{C}}(X,Y)\) of morphisms from \(X\) to \(Y\).
- For every object \(X \in \mathcal{C}\), an identity morphism \(\id_{X} \in \Hom_{\mathcal{C}}(X, X)\).
- For every triple of objects, a composition map \[\Hom_{\mathcal{C}}(X, Y) \times \Hom_{\mathcal{C}}(Y,Z) \to \Hom_{\mathcal{C}}(X, Z)\]
- We have for every morphism \(f: X \to Y\), \(\id_{Y} \circ f = f = f \circ \id_{X}\).
- The composition satisfies the associativity condition.
I will use symbol like \(\cat{Cat}\) to denote categories.
Classifying space
For \(\mathscr{C}\) a small category, the classifying space (or nerve) \(B\mathscr{C}\) isthe Simplicial set with \(B \mathscr{C} = \hom_{\cat{Cat}}(\bm{n}, \mathscr{C})\).
A standard example is the \(BG\), where \(G\) is a group and denoted by the same notion corresponding Groupoid, with one object and morphism \(\Hom(*, *) = G\) and \(\abs{BG}\) is the Eilenberg-Mac Lane space \(K(G,1)\).
Cocomplete
A category is called cocomplete if all Colimits exist.
Referenced: Category CGWH.
TODO Cofiber
Colimit
Let \(C\) be an ∞-category and let \(p: K \to C\) be an arbitrary map of simplicial sets. A colimit for \(p\) is an initial object of \(C_{p/}\). A limit for \(p\) is a final object of \(C_{/p}\).
Referenced: Cocomplete, Compact.
Commutativity constraint
The commutativity constraint is \(\psi_{X,Y}: X \otimes Y \to Y \otimes X\) for all \(X, Y\) such that \[\psi_{Y,X} \circ \psi_{X,Y} = \id_{X \otimes Y}\] with some compatibility condition.
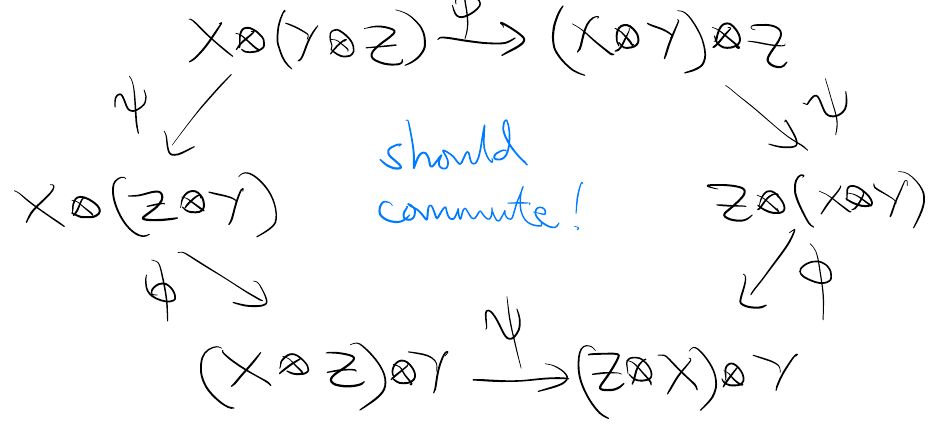
Referenced: Tensor category, Rigid, Tensor functor.
Comodule
Let \(A\) be a Hopf algebra. Then \(V\) with \(k\)-linear map \(\rho: V \to V \otimes A\) satisfying \(V \stackrel{\rho}{\to} V \otimes A \stackrel{\id \otimes \epsilon}{\to} V \otimes k \cong V\) is identity and \(V \stackrel{\rho}{\to} V \otimes A \overset{\rho \otimes \id}{\underset{\id \otimes \Delta}{\rightrightarrows}} V \otimes A \otimes A\) are same.
Compact
An object \(A\) in category \(\mathscr{C}\) is called compact if the functor \(\Hom(A, -): \mathscr{C} \to \cat{Set}\) preserves the Colimit.
An object \(A\) in \(\cat{Set}\) is compact if and only if \(A\) is finite.
Complete
A category is called complete if all Limits exist.
Referenced: Category CGWH.
Complex
A complex of Abelian category \(\mathcal{A}\) is a chain \[A^{\bullet}: \cdots \to A^{-1} \xrightarrow{d^{-1}} A^{0} \xrightarrow{d^{0}} A^{1} \to \cdots\] where the differential satisfies \(d^{k+1} \circ d^{k} = 0\). A morphism between \(A^{\bullet}\) and \(B^{\bullet}\) is a set of morphisms between \(A^{k}\) and \(B^{k}\) commutes with differential map. The category of complexes is denoted by \(C(\mathcal{A})\).
The cohomology of the complex id \(H^{k}(A^{\bullet}) = \frac{\ker d^{k}}{\im d^{k - 1}}\).
We introduce the following associated truncated complexes by \[\tau_{\leq m}A^{\bullet}: \to A^{m -1} \xrightarrow{d^{m - 1}} \ker d^{m} \to 0 \to \] \[\tau^{\leq m}A^{\bullet}: \to A^{m -1} \xrightarrow{d^{m - 1}} A^{m} \xrightarrow{d^{m}} \im d^{m} \to 0 \to\] We also define \[\tau_{\geq m}A^{\bullet} = A^{\bullet}/ \tau_{m -1} A^{\bullet}\] \[\tau^{\geq m}A^{\bullet} = A^{\bullet}/ \tau^{m -1} A^{\bullet}\]
We have shift functor \(X[1]^{i} = X^{i + 1}\).
Acyclic
A complex \(A^{\bullet}\) is called acyclic if \(H^{k}(A^{\bullet}) = 0\) for all \(k \in \ZZ\).
Mapping cone
Let \(u: X^{\bullet} \to Y^{\bullet}\) be a morphism. The mapping cone is the complex given by \(C_{u}^{\bullet} = Y^{\bullet} \oplus (X^{\bullet}[1])\), where \(d_{u}(y, x) = (\dif y + u(x), - \dif x)\). It also denoted by \({\rm Cone}(u)\).
Quasi-isomorphism
A morphism \(u: X^{\bullet} \to Y^{\bullet}\) is a quasi-isomorphism if it induces isomorphism on cohomology groups.
Homotopy
Two complex morphism \(u,v: X^{\bullet} \to Y^{\bullet}\) is called homotopic if there exists a homotopy \(h \in \Hom^{-1}(X^{\bullet}, Y^{\bullet})\) such that \(u - v = \dif_{Y} h + h \dif_{X}\).
Two complexes are homotopy equivalent if there exists \(f: X \to Y\) and \(g: Y \to X\) such that \(v \circ u \sim \id_{X}\) and \(u \circ v \sim \id_{Y}\).
Cone
The left cone \(K^{\vartriangleleft}\) is defined to be \(\Delta^{0} \star K\). And dually, the right cone \(K^{\vartriangleright}\). Either cone contains a distinguished vertex which we will refer to as the cone point.
Cylinder object
A cylinder boject for an object \(A\) in a Closed model category is the commutative triangle
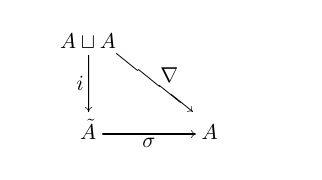 where \(\nabla\) is the canonical fold map identity on each component.
where \(\nabla\) is the canonical fold map identity on each component.
Referenced: Left homotopy, Path object.
Derived category
The derived category of the Abelian category \(\mathcal{A}\) is the Triangulated category \(D(\mathcal{A})\) obtained from the Homotopical category \(K(\mathcal{A})\) by localization with respect to the multiplicative system formed by all the quasi-isomorphisms in \(K(\mathcal{A})\).
We have category \(D^{b}(\mathcal{A})\) (resp. \(D^{+}(\mathcal{A}), D^{-}(\mathcal{A})\)) equivalent to the full triangulated subcategory of \(D(\mathcal{A})\) consisting of objects \(X\) such that \(H^{n}(X) = 0\) for all \(\abs{n} \gg 0\) (resp. \(n \ll 0, n \gg 0\)).
Derived functor
If \(F\) is left exact, we define the right derived functor to be \(RF\) making the diagram commutes and satisfying the universality property.
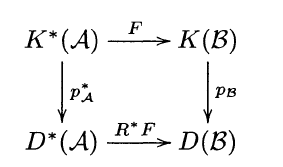
Similarly, we have left derived functor.
Drinfeld double
Let \((H, H^{\vee}, \langle , \rangle)\) Dual pair of Hopf algebra, and let \(H^{0}\) be he Hopf algebra \(H^{\vee}\) with the opposite comultiplication. Then \(D(H) = H \otimes H^{0}\) has an algebra structure uniquely determined by \[\Delta_{D}(a)( R) = R \Delta_{D}^{op}(a)\] for any \(a \in D(H)\) and \(R = \sum_{i} (e_{i} \otimes 1_{H^{0}}) \otimes (1_{H} \otimes e^{i})\), where \(e_{i}\) is basis in \(H\) and \(e^{i}\) basis in \(H^{\vee}\). Such construction is called Drinfeld double.
Dual
We define the dual to be \(X^{\vee} = \ihom(X, U)\), where \(U\) is the Identity object.
Cf. Tensor category.
Referenced: Reflexive.
Essentially surjective
For Simplicial set, a functor is essentially surjective if the induced functor on Homotopy categories is essentially surjective. Similarly statement holds for fully faithful.
Exact
A category is exact if there are Zero object, all the morphisms have kernels and cokernels, and \({\rm Coim}(f) \to {\rm Im}(f)\) is an isomorphism.
F-acyclic
Let \(F: \mathcal{A} \to \mathcal{B}\) be a left Derived functor. An object \(X\) in \(\mathcal{A}\) is F-acyclic if \(R^{i}F = 0\) for all \(i > 0\).
Fiber
Fibre functor
For Tensor category \((\mathscr{C}, \otimes)\), a fibre functor \(F\) is a functor \(\mathscr{C} \to \cat{Vec}\) satisfies that \(F(V_{1} \otimes V_{2}) \cong F(V_{1}) \otimes F(V_{2})\).
Final
An object in Simplicial set is called final if it is final in the Homotopy category. Similar result holds for initial.
Fully faithful
Function complex
The function complex \(\bm{Hom}(X,Y)\) is the simplicial set defined by \[\bm{Hom}(X,Y)_{n} = \hom_{\bm{S}}(X \times \Delta^{n}, Y)\]
Functor
Referenced: Continuous, Simplicial set.
Continuous
Let \(C\) and \(C'\) be Sites with associated Topoi \(T\) and \(T'\), then a Functor \(C' \to C\) is called continuous if for every \(X \in C'\) and \(\{X_{i} \to X\} \in \cat{Cov}(X)\) the family \(\{f(X_{i}) \to f(X)\}\) is in \(\cat{Cov}(f(X))\) and if \(f\) commutes with fiber prooducts when they exists in \(C'\).
Consider \(f: X \to Y\) continuous map, then \(f^{-1}: \cat{Op}(Y) \to \cat{Op}(X)\) is a continuous morhpism of sites.
Given a functor \(f: C' \to C\), we have a functor of presheaves: \(f_{* }: \hat{C} \to \hat{C}'\). That is \((f_{* }F)(T) := F(f(X))\). When functor is continuous, then \(f_{* }\) sends sheaves to sheaves. A functor \(F\) between two categories \(\mathcal{C}\) and \(\mathcal{D}\) is a collection of data, for \(X \in \mathcal{C}\), \(X \to F(X)\) and for \(f \in \Hom_{\mathcal{C}}(X,Y) \to F(f) \in \Hom_{\mathcal{D}}(F(X), F(Y))\) satisfying the associativity and identity condition.
Referenced: Sheaf.
Fully faithful
A functor \(F\) is called fully faithful if \(\Hom(X,Y) \to \Hom(F(X), F(Y))\) is a bijection.
Functorial factorization
A functorial factorization is an ordered pair \((\alpha, \beta)\) of functors \(\cat{Map}(\mathcal{C}) \to \cat{Map}(\mathcal{C})\) such that \(f = \beta(f) \circ \alpha(f)\) for all \(f \in \cat{Map}(\mathcal{C})\).
Referenced: Model category, Cofibrant replacement.
Group object
Groupoid
A groupoid is a category whose morphisms are all isomorphisms.
Referenced: Classifying space, Seifert-Van Kampen theorem.
Heart
Let \((D^{\leq 0}, D^{\geq 0})\) be t-structure for category \(D\), then \(C = D^{\leq 0} \cap D^{\geq 0}\) is called heart of t-structure.
Referenced: Perverse sheaf.
Homotopic
Maps \(f,g\) are a homotopic which is both Left homotopic and right homotopic, denoted by \(f \sim g\).
Homotopical category
We can define the homotopical category of complexes \(K(\mathcal{A})\) with the same object as \(C(\mathcal{A})\) but \(\Hom_{K(\mathcal{A})}(X, Y) = \Hom(X^{\bullet}, Y^{\bullet})/ \sim = H^{0}(\Hom^{\bullet}(X,Y))\).
The family of triangles in \(K(\mathcal{A})\) which are isomorphic to a standard triangle (Mapping cone) is called distinguished triangle.
Homotopy category
Suppose \(\mathcal{C}\) is a category with a subcategory of weak equivalence \(\mathcal{W}\). Define the homotopy category \(\cat{Ho}(\mathcal{C})\) as follows. Form the free category \(F(\mathcal{C}, \mathcal{W}^{-1})\) on the arrows of \(\mathcal{C}\) and reversals of the arrows of \(W\). \(\cat{Ho}(\mathcal{C})\) is the quotient category of \(F(\mathcal{C}, \mathcal{W}^{-1})\) by the relations \(1_{A} = (1_{A})\) for all objects \(A\), \((f, g) = (g \circ f)\) for all composable arrows \(f,g\) and \(1_{\text{dom } w} = (w, w^{-1})\) and \(1_{\text{codom } w} = (w^{-1}, w)\).
Let \(\mathcal{C}_{cf}\) denote the full subcategory of Cofibrant and Fibrant objects of \(\mathcal{C}\). Then we have
The inclusion functor \(\cat{Ho}(\mathcal{C}_{cf}) \to \cat{Ho}(\mathcal{C})\) is equivalence of categories.
Suppose \(\mathcal{C}\) is a model category. Then a map of \(\mathcal{C}_{cf}\) is a weak equivalence if and only if it is a homotopy equivalence.
Cf. Model category, Homotopy equivalence.
Suppose \(\mathcal{C}\) is a model category. Let \(\gamma: \mathcal{C} \to \cat{Ho}(\mathcal{C})\) denote the canonical functor. Let \(Q, R\) denote the cofibrant replacement and fibrant replacement functor.
- The inclusion \(\mathcal{C}_{cf} \to \mathcal{C}\) induces an equivalence of categories \(\mathcal{C}_{cf}/ \sim \cong \cat{Ho}(\mathcal{C}_{cf}) \to \cat{Ho}(\mathcal{C})\).
- There are natural isomorphisms \[\mathcal{C}(QRX, QRY)/ \sim \cat{Ho}(\mathcal{C})(\gamma X, \gamma Y) \cong \mathcal{C}(RQX, RQY)/ \sim\] In addition, there is a natural isomorphism \(\cat{Ho}(\mathcal{C})(\gamma X, \gamma Y) \cong \mathcal{C}(QX, RY)/ \sim\).
- The functor \(\gamma: \mathcal{C} \to \cat{Ho}(\mathcal{C})\) identifies left or right homotopy maps.
- If \(A \to B\) is a map in \(\mathcal{C}\) such that \(\gamma f\) is an isomorphism in \(\cat{Ho}(\mathcal{C})\), then \(f\) is a weak equivalence.
Cf. Cofibrant replacement, Fibrant replacement.
The homotopy category can also be defined for Topological category \(\mathcal{C}\). It is then defined to have the same object \(\mathcal{C}\) and morphism is defined to be \(\Hom_{h \mathcal{C}}(X,Y) = \pi_{0} {\rm Map}_{\mathcal{C}}(X,Y)\), or \({\rm Map}_{h \mathcal{C}}(X,Y) = [{\rm Map}_{\mathcal{C}}(X,Y)]\). The latter denote the equivalence class in Category CGWH by inverting all Weak homotopy equivalence, category \(\mathcal{H}\).
If \(S\) is a simplicial set, then the homotopy category \(hS\) is defined to be the homotopy category \(h \mathfrak{C}[S]\) of Simplicial category \(\mathfrak{C}[S]\). Here \(\mathfrak{C}[S]\) follows the definition of Higher Topos p. 21-22. You can also construct homotopy category by functor \(\pi\), p. 29 Higher Topos.
Homotopy equivalence
A map \(f\) is a homotopy equivalence if there exists a map \(f\) such that \(hf \sim 1\) and \(fh \sim 1\).
Referenced: Homotopy category.
Hopf algebra
A bialgebra \((A, \Delta, \epsilon)\) equipped with an antiautomorphism \(S: A \to A\), that is \(S(ab) = S(b)S(a)\) and \(\Delta(S(a)) = (S \otimes S)(\Delta^{op}(a))\) is called a Hopf algebra if the following diagram is commutative
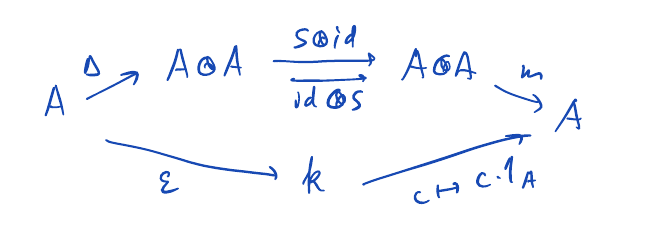
Referenced: Comodule, Drinfeld double, Dual pair, Quasitriangular, Ribbon.
Dual pair
\((H_{1}, H_{2}, \langle \rangle: H_{1} \otimes H_{2} \to k)\) is a dual pair of Hopf algebra if \(\langle, \rangle\) is nondegerate and \[\langle lm, a \rangle = \langle l \otimes m , \Delta_{H_{2}}(a) \rangle\] \[\langle e, ab \rangle = \langle \Delta_{H_{1}}(e), a \otimes b \rangle\] \[\langle S_{H_{1}}(e), a \rangle = \langle e, S_{H_{2}}(a) \rangle\] \[\langle 1_{H_{1}}, a \rangle = \epsilon_{H_{2}}(a)\] \[\langle e, 1_{H_{2}} \rangle = \epsilon_{H_{1}}(e)\]
However, the dual pair is not unique.
Referenced: Drinfeld double.
Quasitriangular
A Hopf algebra \((A, R \in A \hat{\otimes} A)\) is called quasitriangular if \[\Delta^{op}(a) = R \Delta(a)R^{-1}\] \[(\Delta \otimes \id)( R) = R_{13}R_{23} \in A^{\otimes 3}\] \[(\id \otimes \Delta)( R) = R_{13}R_{12} \in A^{\otimes 3}\]
Ribbon
A Hopf algebra is called ribbon if \(v \in Z(A)\) such that \[\Delta_{v} = (v \otimes v)(R_{21}R)^{-1} = (R_{21}R)^{-1}(v \otimes v)\]
Cf. Ribbon category.
Horn
The horn \(\Lambda^{n}_{k}\) is defined by
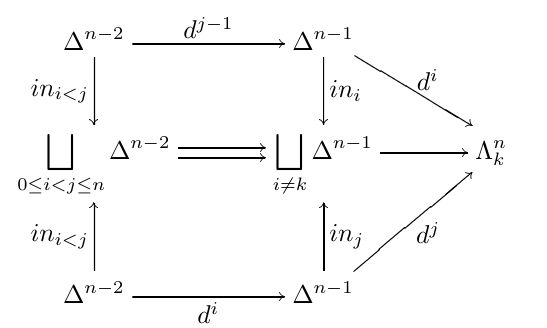 as coequalizer in \(\bm{S}\).
as coequalizer in \(\bm{S}\).
Identity object
See Tensor category.
Referenced: Dual.
Initial
See Final.
Injective
An object \(I\) in an abelian category \(\mathcal{A}\) is injective if the functor \(\Hom(-, I)\) is exact. A complex \(I^{\bullet}\) is injective if all the term \(I^{k}\) are injective.
An abelian category has enough injective objects if any object \(X\) in \(\mathcal{C}\) is a suboject of an injective object \(I\) in \(\mathcal{C}\).
∞-category
We follow Jacob Lurie’s terminology. Joyal call then quasi-categories.
One of the possible candidate for \(\infty\)-category is Topological category, but it is quite hard to work with.
An \(\infty\)-category is a simplicial set \(K\) which has the following property: for any \(0 < i < n\), any map \(f_{0}: \Lambda_{i}^{n} \to K\) admits an extension \(f: \Delta^{n} \to K\).
Cf. Horn.
It is also called weak Kan complexes. (Cf. Kan complex)
The weak Kan complexes approach is equivalent to topological category approach.
The functor (Cf. Functor) between two \(\infty\)-categories is a functor between simplicial sets.
Let \(K\) be an arbitrary simplicial set, and \(C\) a \(\infty\)-category, the simplicial set \({\rm Fun}(K, C)\) is an \(\infty\)-category.
∞-category of spaces
Let \(\cat{Kan}\) denote the full subcategory of \(\cat{Set}_{\Delta}\) spanned by the collection of Kan complex. Then \(S = N(\cat{Kan})\) the Nerve of \(\cat{Kan}\) is called \(\infty\)-category of spaces.
(\infinity,n)-category
A \(\infty,n\)-category is a \(\infty\)-category with \(k\)-morphisms are invertible for \(k > n\).
Internal adjunction
With the notation of Internal Hom, we have internal adjunction \(\ihom(Z, \ihom(X,Y)) \ito \ihom(Z \otimes X, Y)\).
Cf. Tensor category.
Internal Hom
If \(\mathscr{C}^{op} \to \cat{Set}\), \(T \to \Hom(T \otimes X, Y)\) is representable, then write the representing object \(\ihom(X,Y)\) called internal Hom. \(\ihom(T \otimes X, Y) \cong \Hom(T, \ihom(X,Y))\). So we have \({\rm ev}_{X,Y}: \ihom(X, Y) \otimes X \to Y\) isomorphic to \({\rm id}_{\ihom(X,Y)}\).
Cf. Tensor category.
Referenced: Internal adjunction.
Invertible
See Tensor category.
Join
Let \(S\) and \(S'\) be simplicial sets, then the simplicial set \(S \star S'\) is defined as \[(S \start S')(J) = \prod_{J = I \cup I'} S(I) \times S'(I')\] That is \[(S \star S')_{n} = S_{n} \cup S'_{n} \cup \cup_{i + j = n - 1} S_{i} \times S'_{j}\]
If \(S\) and \(S'\) are \(\infty\)-categories, then \(S \star S'\) is an \(\infty\)-category.
Cf. ∞-category.
Left homotopy
A left homotopy of maps \(f,g: A \to B\) is a commutative diagram where \((f, g)\) is the map on the disjoint union. \(\tilde{A}\) is some choice of Cylinder object.
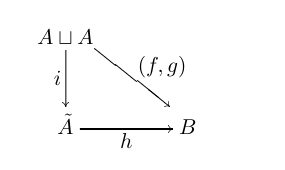
A similar definition of right homotopy for Path object.
Referenced: Homotopic.
Left lifting property
Left Quillen functor
A functor is a left Quillen functor if \(F\) is a left adjoint and preserves cofibrations and trivial cofibrations. A functor is a right Quillen functor if \(U\) is a right adjoint and preserves fibrations and trivial fibrations. We call \((F, U, \phi)\) Quillen adjunction if \(F\) is a left Quillen functor and \(\phi\) makes \(U\) a right adjoint of \(F\).
Referenced: Quillen adjunction, Right Quillen functor, Total left derived functor.
Limit
See Colimit.
Referenced: Complete.
Map
For a category \(\mathcal{C}\), we can form a category \(\cat{Map}(\mathcal{C})\), whose objects are morphisms of \(\mathcal{C}\) and whose morphisms are commutative squares.
For \(S\) simplicial subset containing vertices \(x\) and \(y\). We define \({\rm Map}_{S}(x,y) = {\rm Map}_{hS}(x,y) \in \mathcal{H}\) to be the object of \(\mathcal{H}\) representing the space of maps from \(x\) to \(y\) in \(S\).
Model category
A model structure on a category is three classes of morphisms called cofibrations, fibrations, and weak equivalences, satisfying
The category is closed under all finite limits and colimits.
Suppose that the following diagram commutes,
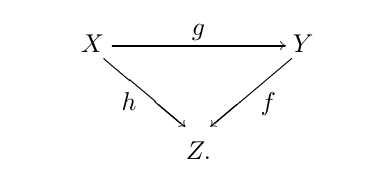 if any two \(f, g\) and \(h\) are weak equivalence, then so is the third.
if any two \(f, g\) and \(h\) are weak equivalence, then so is the third.If \(f\) is a Retract of \(g\) and \(g\) is a weak ewquivalence, fibration or cofibration, then so if \(f\).
Suppose that we are given a commutative solid arrow diagram
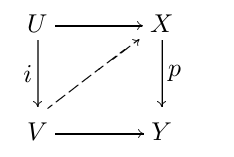 where \(i\) is a cofibration and \(p\) is a fibration. Then the dotted arrow exists, making the diagram commute, if either \(i\) or \(p\) is also a weak equivalence.
where \(i\) is a cofibration and \(p\) is a fibration. Then the dotted arrow exists, making the diagram commute, if either \(i\) or \(p\) is also a weak equivalence.Any map \(f: X \to Y\) may be factored \(f = p \circ i\), where \(p\) is fibration and \(i\) is trivial cofibration and \(f = q \circ j\) where \(q\) is a trivial fibration and \(j\) a cofibration. (We can further require Functorial factorization)
A model category is a category with all small limits and colimits together with a model structure.
The definition of a model category here differs from definition in Quillen’s original definition. It is roughly called closed model category there. For more differences, you can see book Model categories by Hover.
If \(\mathcal{C}\) is a model category, then it has an initial object, the colimit of the empty diagram, and a terminal object, the limit of the empty diagram.
Referenced: Cylinder object, Homotopy category, Cofibrant, Path object.
Cofibrant
An object of Model category is called cofibrant if the map from the initial object \(0\) to it is a cofibration.
An object is called fibrant if the map from it to the terminal object is a fibration.
Referenced: Homotopy category, Fibrant, Cofibrant replacement, Quillen equivalence, Total left derived functor.
Fibrant
See Cofibrant.
Referenced: Homotopy category, Quillen equivalence.
Fibrant replacement
Referenced: Homotopy category.
Cofibrant replacement
By applying factorization to \(0 \to X\), we get a cofibrant replacement functor \(X \to QX\) (Functorial factorization is required here) such that \(QX\) is Cofibrant and \(QX \to X\) is a trivial fibration.
Similar, we have fibrant replacement functor \(X \to RX\) by applying factorization to \(X \to 1\).
Referenced: Homotopy category, Fibrant replacement.
Monoid
A monoid is a group without inverse. In other words, a group is a monoid with inverse.
Monoidal category
A monoidal category is a category \(C\) with \(\otimes\) which has Associativity constraint and there exists unit \(1 \in \mathop{Ob}( C)\) such that \(1 \otimes V \cong V \otimes 1 \cong V\).
A monoidal functor is a functor respect the monoid structure.
Cf. Tensor category. In fact, I don’t know their differences.
Referenced: Strict, Pivotal, Braided, Rigid braided monoidal category.
Strict
A Monoidal category is called strict if \((A \otimes B) \otimes C = A \otimes (B \otimes C)\) and the same is for morphisms.
Every monoidal category \(C\) is naturally equivalent to a strict monoidal category \(C^{str}\)
Pivotal
A Rigid Monoidal category is called pivotal if there exists a system of functorial isomorphism \[\mu = \{\mu_{X}: X \to X^{**}\}\] such that \[\mu_{X \otimes Y} = \mu_{X} \otimes \mu_{Y}\]
Referenced: Spherical.
Trace
We introduce the categorical trace by \[\tr_{f}^{L} = 1 \xrightarrow{i} V \otimes V^{*} \xrightarrow{f \otimes \id} V \otimes V^{*} \xrightarrow{\mu_{V} \otimes \id} V^{**} \otimes V^{*} \xrightarrow{e_{V^{*}}} 1\] Similarly, we can define the right trace \(\tr_{f}^{R}\).
We have following properties similar to classical trace \(\tr^{L,R}(fg) = \tr^{L,R}(gf)\) and \(\tr^{L,R}(f \otimes g) = \tr^{L,R}(f) \otimes \tr^{L,R}(g)\).
Referenced: Spherical, Dimension.
Spherical
A Pivotal category is spherical if for any \(V\) and \(f: V \to V\), we have \(\tr^{L}(f) = \tr^{R}(f)\).
Cf. Trace.
Referenced: Dimension.
Dimension
In Spherical category we can define the categorical dimension by \(\dim V = \tr(\id_{V})\) since the two Traces are the same.
Braided
A Monoidal category is braided if there exists \(c = \{c_{V,W}\}\), \(c_{V,W}: V \otimes W \to W \otimes V\) with some compatibility conditions.
Referenced: Rigid braided monoidal category.
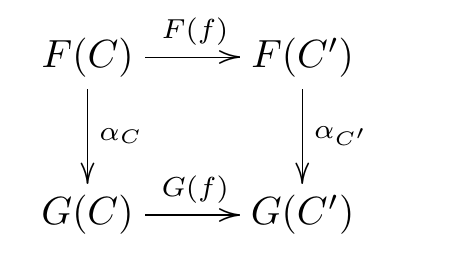
Natural transformation
A natural transformation \(\alpha\) between two Functors \(F,G: \mathcal{C} \to \mathcal{D}\) is a collection of morphisms \(\{\alpha_{C}: F( C) \to G( C)\}_{C \in \mathcal{C}}\) satisfying the commutative diagram
Nerve
To any category \(\mathcal{C}\), we can associate a Simplicial set \(N(\mathcal{C})\) called nerve of \(\mathcal{C}\). For each \(n \geq 0\), we let \(N(\mathcal{C})_{n} = {\rm Map}_{\cat{Set}_{\Delta}}(\Delta^{n}, N(\mathcal{C}))\) denote the set of all functors \([n] \to \mathcal{C}\).
The objects of \(\mathcal{C}\) are simply the vertices of \(N(\mathcal{C})\).
There exists a useful characterisation of the nerve.
Let \(K\) be a simplicial set. Then the following conditions are equivalent:
There exists a small category \(\mathcal{C}\) and an isomorphism \(K \cong N(\mathcal{C})\).
For each \(0 < i < n\) and each diagram
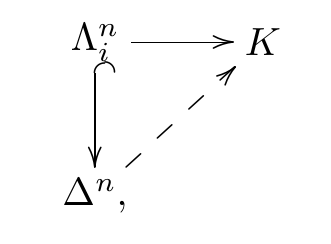 there exists a unique dotted arrow rendering the diagram commutative.
there exists a unique dotted arrow rendering the diagram commutative.
The nerve functor \(\cat{Cat} \to \cat{Set}_{\Delta}\) is right adjoint to the functor \(h: \cat{Set}_{\Delta} \to \cat{Cat}\), which associates to every simplicial set \(S\) its homotopy category \(hS\).
Cf. Homotopy category.
Ordinal number category
See Simplicial set.
Overcategory
See the following diagram of overcategory
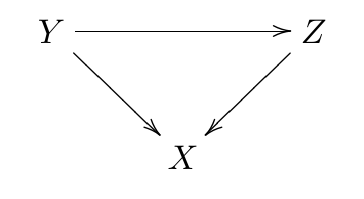
For any category \(C'\), we have bijection \[\Hom(C', C_{/X}) \con \Hom_{x}(C' \star [0], C)\] where \(x: [0] \to [C]\) is the canonical functor.
Cf. Join.
Let \(S\) and \(K\) be simplicial sets, and \(p: K \to S\) an arbitrary map. There exists a simplical set \(S_{/p}\) with the following universal property: \[\Hom_{\cat{Set}_{\Delta}}(Y, S_{/p}) = \Hom_{p}(Y \star K, S)\] where the subscript on the right side, means \(f|_{K} = p\).
One defines \((S_{/p})_{n}\) to be \(\Hom_{p}(\Delta^{n} \star K, S)\).
\(C_{/p}\) is an \(\infty\)-category.
\(N( C)_{/X} \cong N(C_{/X})\)
Path object
Let \(\bm{S}_{f}\) be the full subcategory of Simplicial set category (or Closed model category) whose objects are the Kan complex. A path object for \(X \in \bm{S}_{f}\) is a commutative diagram
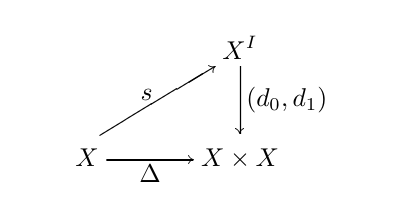
where \(s\) is a Weak equivalence and \(d_{0}, d_{1}\) are Kan fibrations (in fact necessarily Trivial fibrations).
Cf. Cylinder object.
Referenced: Left homotopy.
Pointed
An category is called pointed if the map from the initial object to the termninal object is an isomorphism.
Quillen adjunction
Cf. Left Quillen functor.
Referenced: Quillen equivalence.
Quillen equivalence
A Quillen adjunction \((F, U, \phi): \mathcal{C} \to \mathcal{D}\) is called a Quillen equivalence if and only if, for all Cofibrant \(X\) in \(\mathcal{C}\) and Fibrant \(Y\) in \(\mathcal{D}\), a map \(f: FX \to Y\) is a weak equivalence in \(\mathcal{D}\) if and only if \(\phi(f): X \to UY\) is a weak equivalence in \(\mathcal{C}\).
Reflexive
An object \(X\) is called reflexive if \(i_{X}: X \ito X^{\vee \vee}\).
Cf. Dual, Tensor category.
Referenced: Rigid.
Representable
We say that a functor \(F: \cat{Sch} \to \cat{Sets}\) is representable by a scheme if there exists a scheme \(X\) and an isomorphism of functors \(F \cong h_{X}\). A morphism \(F \to G\) of functors is representable by schemes if for any map \(S \to G\) from a scheme \(S\), the fiber product \(F \times_{G} S\) is representable by a scheme.
A morphism \(F \to G\) is open immersion if for any morphism \(S \to G\) from a scheme \(S\), \(F \times_{G} S\) is representable by an open subscheme of \(S\).
We say that a set of open subfunctors \(\{F_{i}\}\) is a Zariski-open cover of \(F\) if for any morphism \(S \to F\) from a scheme \(S\), \(\{F_{i} \times_{F} S\}\) is a Zariski-open cover of \(S\).
If we have\(F \cong h_{X}\), then the universal family of \(F\) is the object \(U \in F(X)\) corresponding to the identity morphism \(\id_{X}\)
A morphism \(X \to Y\) of Prestacks over \(\cat{Sch}\) is representable if for every morphism \(V \to Y\) form a scheme \(V\), the fiber product \(X \times_{Y} V\) is an Algebraic space.
.
Retract
A map in \(\mathcal{C}\) is a retract of a map \(g \in \mathcal{C}\) if and only if there is a commutative diagram of the form
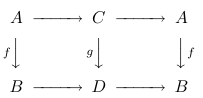
where horizontal composites are identities.
Referenced: Model category.
Ribbon category
A ribbon category is a Rigid braided monoidal category with \(v = \{v_{X}\}\) such that \[v_{X \otimes Y} = (v_{X} \otimes v_{Y}) c_{XY}^{-1}c_{YX}^{-1}\]
Referenced: Ribbon.
Right lifting property
A map \(p: X \to Y\) is said to have the right lifting property (RLP) with repsect to a class \(M\) is in every solid arrow diagram
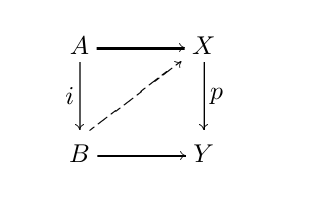 with \(i \in M\) the dotted arrow exists making the diagram commute.
with \(i \in M\) the dotted arrow exists making the diagram commute.
The left lifting property is defined by same diagram with \(i\) and \(p\) in definition changed.
Referenced: Left lifting property, Kan fibration.
Right morphism
For \(S\) ∞-category, we define right morphism from \(x\) to \(y\) to be a new simplicial set \(\Hom_{S}^{R}(x,y)\), by letting \(\Hom_{\cat{Set}_{\Delta}}(\Delta^{n}, \Hom_{S}^{R}(x,y))\) denote the set of all \(z: \Delta^{n + 1} \to S\) such that \(z| \Delta^{n + 1} = y\) and \(z| \Delta^{0, \cdots, n}\) is a constant simplex at the vertex \(x\).
The simplicial set \(\Hom_{C}^{R}(x,y)\) is a Kan complex.
Cf. Kan complex.
Right Quillen functor
See Left Quillen functor.
Rigid braided monoidal category
A rigid braided monoidal category is a Rigid Braided Monoidal category such that \[c_{A^{*}B^{*}} = (c_{B,A})^{*}\]
Referenced: Ribbon category.
Saturated
A class \(M\) of monomorphisms of \(\cat{S}\) is said to be saturated if the following conditions are satisfied:
- All isomorphisms are in \(M\).
- \(M\) is closed under pushout.
- Each retract of an element of \(M\) is in \(M\).
- \(M\) is closed under countable compositions and arbitrary direct sums.
Simplicial category
A simplicial category is a category which is enriched over the category \(\cat{Set}_{\Delta}\) of simplical sets. The category of simplicial categories will be denoted by \(\cat{Cat}_{\Delta}\).
A functor \(\mathcal{C} \to \mathcal{C}'\) between simplicial categories is an equivalence if the induced functor \(h \mathcal{C} \to h \mathcal{C}'\) is an equivalence of \(\mathcal{H}\)-enriched categories.
Simplicial group
A simplicial group is a simplical object in the category of groups, that is a contravariant functor from \(\bm{\Delta}\) to the category \(\cat{Group}\).
Simplicial homotopy
Let \(f, g: K \to X\) be simplicial maps. We say that there is a simplicial homotopy \(f \cong g\) from \(f\) to \(g\) if there is a commutative diagram
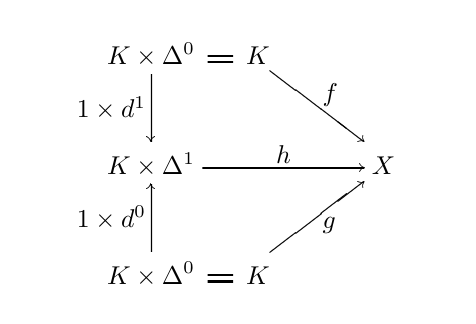
The map \(h\) is called homotopy.
This is the analog of topological Homotopy.
Simplicial homotopy group
Let \(X\) be a Fibrant Simplicial set and \(v \in X_{0}\) be a vertex of \(X\). Define the simplicial homotopy group \(\pi_{n}(X, v), n \geq 1\) to be the set of homotopy classes of maps \(\alpha: \Delta^{n} \to X (\text{rel } \partial \Delta^{n})\) fit into the diagram
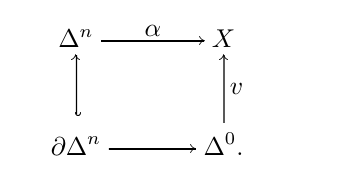
\(\pi_{0}(X)\) is usually called path components of \(X\). The simplicial set \(X\) is said to be connected if \(\pi_{0}(X)\) is trivial.
\(\pi_{n}(X, v)\) is a group for \(n \geq 1\) and abelian group for \(n \geq 2\).
The group law is given by \([\alpha] * [\beta]\) to be \(\dif_{n}(\omega)\) of the extension
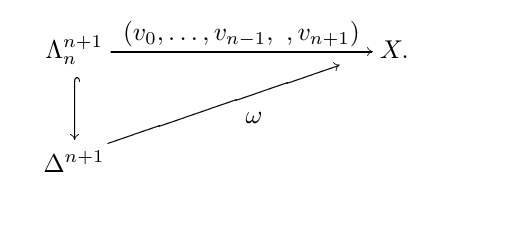 where \((v_{0}, \cdots, v_{n - 1}, , v_{n+1}) = (v, v, \cdots, v, \alpha, , \beta)\).
where \((v_{0}, \cdots, v_{n - 1}, , v_{n+1}) = (v, v, \cdots, v, \alpha, , \beta)\).
Cf. Homotopy group.
Simplicial set
Let \(\bm{\Delta}\) be the category of finite ordianl numbers with order preserving maps between them. The object of \(\bm{\Delta}\) is denoted by \(\bm{n}\) which is a category denoted by \(0 \to 1 \to 2 \to \cdots \to n\), where identity and composition morphism is omitted. \(\bm{\Delta}\) is called ordinal number category. A simplicial set is a contravariant Functor \(X: \bm{\Delta^{op}} \to \cat{Sets}\).
One of the important example is standard covarinat functor \(\bm{\Delta} \to \cat{Top}\) mapping \(\bm{n}\) to standard n-simplex \(\abs{\Delta^{n}}\) with \[\abs{\Delta^{n}} = \{(t_{0}, \cdots, t_{n}) \in \RR^{n + 1} \mid \sum_{i = 0}^{n}t_{i} = 1, t_{i} \geq 0\}\]
In this language, the Singular homology can be describe by singular set \(S(T)\) \[\bm{n} \to \hom(\abs{\Delta^{n}, T})\]
We have morphism in \(\bm{\Delta}\) \(d_{i}: \bm{n - 1} \to \bm{n}\) (cofaces) and \(s^{j}: \bm{n + 1} \to \bm{n}\) (codegeneracies), defined as \[d^{i}(0 \to 1 \to \cdots \to n - 1) = (0 \to 1 \to \cdots \to i - 1 \to i + 1 \to \cdots \to n)\] \[s^{j}(0 \to 1 \to \cdots \to n + 1) = (0 \to 1 \to \cdots \to j \to j \to \cdots \to n)\]
We have cosimplicial identities
\begin{align*} \begin{cases} d^{j}d^{i} = d^{i}d^{j - 1} & \text{if } i < j \\ s^{j}d^{i} = d^{i}s^{j - 1} & \text{if } i < j \\ s^{j}d^{j} =1 = s^{j}d^{j+1} &\\ s^{j}d^{i} = d^{i - 1} s^{j} & \text{if } i > j + 1 \\ s^{j}d^{i} = s^{i}s^{j+1} & \text{if } i \leq j \\ \end{cases} \end{align*}
We have similar simplicial identities for \(Y_{n}\), where \(Y\) is a simplicial set.
Referenced: Classifying space, Ordinal number category, Path object, Simplicial homotopy group, Realization, Fibrant, Weak equivalence.
Realization
A realization of a Simplicial set \(X\), \(\abs{X}\), is defined to be \[\abs{X} = \varinjlim_{\Delta^{n} \to X} \abs{\Delta^{n}}\] It is a functor from simplicial set category to topology space category (in fact \(\cat{CGWH}\), Category CGWH). In fact, we have adjoint property \[\hom_{\cat{Top}}(\abs{X}, Y) \cong \hom_{\cat{S}} (X, SY)\]
Kan fibration
A map \(p: X \to Y\) of simplicial set is called Kan fibration if it satisfies the extension condition that for every commutative diagram
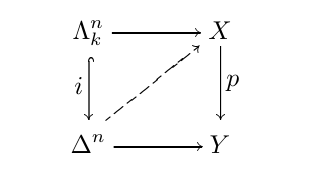 there exists \(\theta: \Delta \to X\) making the diagram commute.
there exists \(\theta: \Delta \to X\) making the diagram commute.
Kan fibration is the categorical analog of Fibration.
A Kan fibration is a map which has the right lifting property with respect to all anodyne extensions.
Cf. Anodyne extension, Right lifting property.
Referenced: Path object, Fibrant, Trivial fibration.
Fibrant
A Simplicial set is called fibrant or Kan complex if the canonical map \(Y \to *\) is a Kan fibration.
Referenced: Simplicial homotopy group, Kan complex, Weak equivalence.
Kan complex
See Fibrant.
Referenced: Path object.
Weak equivalence
The map \(f: X \to Y\) between Fibrant Simplicial sets is called weak equivalence if
- For each vertex \(x\) of \(X\) the induced map \(f_{*}: \pi_{i}(X, x) \to \pi_{i}(Y, f(x))\) is an isomorphism for \(i \geq 1\).
- The map \(f_{*}: \pi_{0}(X) \to \pi_{0}(Y)\) is a bijection.
Cf. Weak homotopy equivalence.
Referenced: Path object, Trivial fibration.
Trivial fibration
A map \(p: X \to Y\) in \(\bm{S}_{f}\) is called trivial fibration if it is a Kan fibration and a Weak equivalence.
Referenced: Path object.
TODO Stable ∞-category
Strongly final
Let \(\mathcal{C}\) be a Simplicial set, then a vertex \(X\) is strongly final if the projection \(\mathcal{C}_{/X} \to \mathcal{C}\) is a trivial fibration of simplicial sets. That is for any map \(\f_{0}: \partial \Delta^{n} \to \mathcal{C}\) such that \(f_{0}(n) = X\) can be extended to a map \(f: \Delta^{n} \to \mathcal{C}\).
Let \(\mathcal{C}\) be an \(\infty\)-category containing an object \(Y\). The object \(Y\) is strongly final if and only if for every object \(X \in \mathcal{C}\) the Kan complex \(\Hom_{\mathcal{C}}^{R}(X, Y)\) is contractible.
Cf. ∞-category.
Let \(\mathcal{C}\) be a simplicial set. Every strongly final object of \(\mathcal{C}\) is final object of \(\mathcal{C}\). The converse holds if \(\mathcal{C}\) is an \(\infty\)-category.
Cf. Final.
The discussion can be generalized to Initial.
Tensor category
A tensor category is data \((\mathscr{C}, \otimes, \phi, \psi)\) where \(\phi\) is the Associativity constraint and \(\psi\) the Commutativity constraint.
The identity object in tensor cateogry is a pair \((U, u)\) where \(U \in \mathscr{C}\) with \(u: U \ito U \otimes U\) such that \(U \otimes -\) is an equivalence.
The object \(L\) is called invertible if \(L \otimes -\) is an equivalence. If \(L\) is invertible, then \(L\) has inverse with \(\delta: L \otimes L^{-1} \ito U\).
Referenced: Dual, Fibre functor, Identity object, Internal adjunction, Internal Hom, Invertible, Monoidal category, Reflexive, Rigid, Tensor functor, Criterion for category being representation category.
Rigid
A Tensor category is called rigid if we have isomorphism \[\ihom(X_{1}, Y_{1}) \otimes \ihom(X_{2}, Y_{2}) \to \ihom(X_{1} \otimes X_{2}, Y_{1} \otimes Y_{2})\] for all \(X_{i}, Y_{i}\) and all objects are Reflexive.
In rigid category, we have trace \(ihom(X, X) \to X^{\vee} \otimes X \to U\) called trace. And we define the rank to be \(\tr_{X}({\rm id}_{X})\).
The following is a criterion for rigidity.
Let \(C\) be an abelian category and \(\otimes: C \times C \to C\) bilinear. Take \[F: C \to \cat{Vec}_{k}\] faithul exact and \(\phi, \psi\) isomorphisms of associativity and communitivity such that
- \(F\) repsects \(\otimes\).
- \(F\) induces usual associativitiy on \(\cat{Vec}_{k}\).
- \(F\) induces usual communitivity on \(\cat{Vec}_{k}\).
- There exists identity \(U\) in \(C\) where \(k \cong \End(U)\) and \(\dim F(U) = 1\).
- If \(\dim F(L) = 1\), then there exists \(L^{-1}\) such that \(L \otimes L^{-1} \cong U\).
Then \((C, \otimes)\) is abelian rigid tensor category.
Cf. Associativity constraint, Commutativity constraint, Tensor category.
Referenced: Pivotal, Rigid braided monoidal category, Criterion for category being representation category.
Tensor functor
A tensor functor between Tensor category is a functor with morphism \[c:FX \otimes FY \ito F(X \otimes Y)\] functorial in \(X, Y\) with compatibility with Commutativity constraint and Associativity constraint.
t-exact
A functor is called t-exact if it is compatible with the t-structure.
Topological category
A topological category is a category which is enriched over \(\cat{CGWH}\). The category of topological category will be denoted by \(\cat{Cat}_{top}\).
Cf. Category CGWH.
Torsion pair
A torsion pair \((\mathcal{P}, \mathcal{Q})\) is a pair of full subcategory of \(\mathcal{C}\) such that
- \(\hom(P, Q) = 0\) for every \(P \in \mathcal{P}, Q \in \mathcal{Q}\).
- \(\hom(\mathcal{P}, X) = 0\), then \(X \in \mathcal{Q}\).
- \(\hom(X, \mathcal{Q}) = 0\), then \(X \in \mathcal{P}\).
- For every \(C\) in \(\mathcal{C}\), there exists \(P \in \mathcal{P}, Q \in \mathcal{Q}\) such that \[0 \to P \to C \to Q \to 0\] is exact.
Total left derived functor
If \(F: \mathcal{C} \to \mathcal{D}\) is a Left Quillen functor, define the total left derived functor \(LF: \cat{Ho}(\mathcal{C}) \to \cat{Ho}(\mathcal{D})\) to be the composite \[\cat{Ho}(\mathcal{C}) \xrightarrow{\cat{Ho}(Q)} \cat{Ho}(\mathcal{C}_{c}) \xrightarrow{\cat{Ho}(F)} \cat{Ho}(\mathcal{D})\] where \(\mathcal{C}_{c}\) means the full subcategory with Cofibrant objects. For natural transformation, we have total derived natural transformation.
Similarly, we have total right derived functor.
Referenced: Total right derived functor.
Total right derived functor
See Total left derived functor.
Triangulated category
An Additive category \(\mathcal{C}\) endowed with a shift self-equivalence \(T\) and a family of distinguished triangles \(\mathcal{T}\) is a triangulated category if these data satisfying the following axioms, with \(X[1] = TX\).
Any triangle isomprhic to a distinguished triangle is distinguished.
\(X \to X \to 0 \to \) is distinguished.
Any \(u: X \to Y\) is part of distinguished triangle \(X \to Y \to Z \to \).
A triangle \(X \to Y \to Z \to \) is distinguished if and only if the triangle \(Y \to Z \to X[1] \to\) is distinguished.
Any diagram
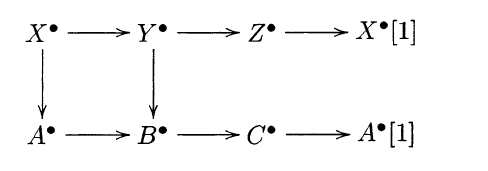 can be completed to commutative diagram.
can be completed to commutative diagram.For any pair of morphism \(u: X \to Y\) and \(v: Y \to Z\) and triple \(X \to Y \to A \to \) \(Y \to Z \to B \to \) and \(X \to Z \to C \to X\) there are isomorphisms \(a: A \to C\), \(b: C \to B\) and the triangle \(A \to C \to B \to A\) is distinguished.
A full additive subcategory \(\mathcal{D} \subset \mathcal{C}\) is called a triangulated subcategory if \(T(\mathcal{D}) \subset \mathcal{D}\) and if two vertices in a distinguished triangle in \(\mathcal{T}\) are in \(\mathcal{D}\), then so is the third.
Referenced: t-structure.
t-structure
Let \(D\) be a Triangulated category and \(D^{\leq 0}, D^{\geq 0}\) full subcategories, then \((D^{\leq 0}, D^{\geq 0})\) is called t-structure if the followings are satisfied
- \(D^{\leq 1} \subset D^{\leq 0}\), \(D^{\geq 1} \subset D^{\geq 0}\).
- \(\Hom_{D}(X, Y) = 0\) for \(X \in D^{\leq 0}, Y \in D^{\geq 1}\).
- For \(X \in D\), there exists distinguished triangle \[X_{0} \in D^{\leq 0} \to X \to X_{1} \in D^{\geq 1} \to X_{0}[1]\]
Referenced: Heart, t-exact, Bounded, Perverse sheaf.
Bounded
A t-structure is called bounded if \(D^{\leq n} = D = D^{\geq m}\) for \(m \ll 0\) and \(n \gg 0\).
Undercategory
Cf. Overcategory.
Weak equivalence
Let \(F: \mathcal{C} \to \mathcal{D}\) be functor between Topological categories, we say that \(F\) is a weak equivalence (or equivalence) if the induced functor \(h \mathcal{C} \to h \mathcal{D}\) is an equivalence of \(\mathcal{H}\)-enriched categories.
Cf. Homotopy category.
TODO Zero object
Commutative Algebra
TODO Commutative Frobenius algebra
Ext group
Let \(M, N\) be two \(R\)-modules. Let \(P_{\bullet} \to M\) be a free \(R\)-module resolution of \(M\) \[\cdots \to P_{n} \to \cdots \to P_{1} \to P_{0} \to M \to 0\] is an exact sequence of \(R\)-modules and \(P_{i}\)’s are free. Then we define the Ext group by \[\Ext^{k}_{R}(M, N) = H^{k}(\Hom(P_{\bullet}, N))\] and the Tor group \[\Tor^{R}_{k}(M, N) = H_{k}(P_{\bullet} \otimes_{R} N)\]
Referenced: Tor group.
TODO Finite length
TODO K-theory
Module
TODO Injective
TODO Resolution
Semisimple
An object in a category is called semisimple if it is the direct sum of the Simple object.
TODO Simple
Referenced: Semisimple.
Tor group
See Ext group.
Sheaf Theory
Constructible sheaf
A sheaf is called constructible if \(F|_{X_{\alpha}}\) is a Local system for some Stratification \((X_{\alpha})\). And we define the category \(D_{c}^{b}(X) \subset D^{b}(X)\) full subcategory with constructible cohomology.
Dual complex
We define dual complex to be \(D_{X} = w_{X}[n]\), where \(n = \dim X\). and \(w_{X}(U) = \Hom(H_{c}^{n}(U), k)\).
Referenced: Verdier duality.
TODO Equivariant sheaf
TODO G-resolution
Equivariant pullback
TODO Intersection cohomology
TODO Local system
The local system also has its dual.
Referenced: Constructible sheaf, Verdier duality.
Perverse sheaf
For \(D = D^{b}_{c}(X)\), we can take t-structure as \[D^{\leq 0} = \{F | \dim \supp \mathscr{H}^{j}(F) \leq -j\}\] \[D^{\geq 0} = \{F | \dim \supp \mathscr{H}^{j}(\mathbb{D}_{X}F) \leq -j\}\] And we define the perverse sheaf to be the Heart of the t-structure. That is \[\cat{Perv}(X) = D^{\leq 0} \cap D^{\geq 0}\]
The operator \(\mathbb{D}_{X}\) preverse the category \(\cat{Perv}(X)\).
For perverse sheaf category, we have functor \(^{p}F\).
TODO Six functors
\(f^{-1}\) is exact, and \(f_{* }\) and \(f_{!}\) only left exact.
We have following important properties for operators.
Adjunction pairs: \((f^{*}, Rf_{* })\), \((Rf_{!}, f^{!})\), \((- \otimes \mathcal{F}, \shom(\mathcal{F}, -)\).
The morphism between functors \(f_{!} \to f_{* }\), which is isomorphism if \(f\) is proper. Also, we have \(j^{!} = j^{* }\) for \(j\) an open inclusion.
For \(X = U \coprod Z\) where \(U\) is open and \(Z\) is closed, denote the includion \(i: U \to X\), \(j: Z \to X\), then we have distinguished triangles \[i_{!}i^{!} \to \id \to j_{* } j^{* }\] \[j_{!}j^{!} \to \id \to i_{* } i^{* }\]
See Verdier duality.
For \(f: X \to Y\) smooth of relative dimension \(d\) then one has an isomorphism \[f^{!}k = k[2d]\]
\(H^{n}(X) = H^{n}(f_{* }k_{X})\), \(H_{n}^{!}(X) = H^{n}(f_{* } \omega_{X})\), \(H_{!}^{n} = H^{n}(f_{!}k_{X})\), \(H_{n}(X) = H^{-n}(f_{!} \omega_{X})\)
For pullback diagram
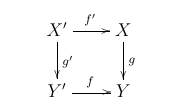 We have isomorphism of functors
\[f^{* } \circ g_{!} \cong (g')_{!} \circ (f')^{!}\]
We have isomorphism of functors
\[f^{* } \circ g_{!} \cong (g')_{!} \circ (f')^{!}\]
Stratification
A stratification of \(X\) is a decomposition \[X = \coprod_{\alpha \in A} X_{\alpha}\] which is locally finite, \(X_{\alpha}\) locally closed and smooth and satisfies \[\bar{X}_{\alpha} = \coprod_{\beta \in B} X_{\beta}\]
Referenced: Constructible sheaf.
Verdier duality
Let \(D_{X} \in D^{b}(X)\) be the Dual complex, we define \(\mathbb{D}_{X}(E) = \mathbb{R} \shom_{X}(E, D_{X})\) gives functor \(\mathbb{D}_{X}: D^{b}(X) \to D^{b}(X)\).
We have \(\mathbb{D}^{2} = \id\).
The Verdier duality is the eqauility \[\mathbb{D}_{Y} \circ Rf_{!} = Rf_{*} \circ \mathbb{D}_{X}\] Also, we have \[f^{!} \circ \mathbb{D}_{Y} = \mathbb{D}_{X} \circ f^{-1}\]
As a speical case, when \(\mathcal{L}\) is Local system and \(X\) is smooth, we have \[\mathbb{D} \mathcal{L} \cong \mathcal{L}^{\vee}[2 d_{X}]\]
Referenced: Six functors.
TODO Whitney stratification
Representation theory
The reference of representation of finite groups includes [steinberg2012] Chapter 1-6. The basics of the quivers are from [kirillov2016].
Burnside Theorem
Let \(G\) be a group of order \(p^{a}q^{b}\) with \(p\), \(q\) primes. Then \(G\) is not simple unless it is cyclic of prime order.
TODO Characters
\(L(G)\); character; irreducible character; class function; multiplicity; regular representation; character table
Equivalent representations has equal characters.
Characters are class functions.
The irreducible characters of \(G\) form an orthonormal set of class functions. and \({\rm dim} Z(L(G)) = |Cl(G)|\). Therefore the number of irreducible representations is smaller than the conjugacy groups. In fact, two numbers are equal.
\(|G| = d_{1}^{2} + d_{2}^{2} + \cdots + d_{s}^{2}\) holds, where \(d_{i}\) is the degree of the irreducible representation.
Cf. Orthogonal relations.
Let \(C\), \(C'\) be conjugacy classes of \(G\), and let \(g \in C\) and \(h \in C'\). Then
\begin{equation} \sum_{i = 1}^{s}\chi_{i}(g) \overline{\chi_{i}(h)} = \begin{cases} |G|/|C| & C = C' \\ 0 & C \neq C' \end{cases} \end{equation}
That is the columns of the character table are orthogonal.
TODO Class function
Completely decomposition
Every representation of a finite group is equivalent to a unitary representation.
Every representation of a finite group is completely reducible.
Criterion for category being representation category
Let \((C, \otimes)\) rigid abelian tensor category, \(\End({\bold 1}) = k\) and \(w: C \to \cat{Vec}_{k}\) exact faithful \(k\)-linear tensor functor. Then we have
- \(\cat{Aut}^{\otimes}(w) \cong G\) affine group scheme.
- \(C \to \cat{Rep}_{k}(G)\) induced by \(w\) is tensor equivalence.
Cf. Tensor category, Rigid, Group scheme.
Dimension theorem
Let \(\phi\) be an irreducible representation of \(G\) of degree \(d\). Then \(d\) divides \(|G|\).
这里值得注意的是,证明中使用了一些代数数论的结论,主要是关于 algebraic number 和 algebraic integer。
Fourier analysis of finite groups
fourier transform; fourier inversion; convolution; dual group;
The class functions form the center of \(L(G)\).
\(\widehat{a * b} = \hat{a} \cdot \hat{b}\)
nonabelian Fourier transform (Wedderburn)
Orthogonal relations
Group algebra
Suppose that \(\phi,\rho: G \to U_{n}( C)\) are inequivalent irreducible unitary representations. Then
\begin{equation} \langle \phi_{ij}, \rho_{kl} \rangle = 0 \end{equation}
\begin{equation} \langle \phi_{ij}, \phi_{kl} \rangle = \begin{cases} 1/n & \text{if } i = k \text{ and } j = l \\ 0 & \text{else} \end{cases} \end{equation}
Referenced: Characters and class functions.
Point group
A finite subgroup of O(3) is called a point group.
Quivers
quiver; subquiver; oriented cycle; loop; morphism; direct sum; subrepresentation; irreducible representation; indecomposable representation; quivers of finite type; path; product of path; path algebra; one-way path
The category of representations of \(Q\) over a field \(k\) is equivalent to the category of \(k(Q)\)-modules.
The Jacobson radical of the path algebra \(k(Q)\) is the span of all one-way paths of \(Q\).
Reconstruction theorem
Let \(\cat{Rep}_{k}(G)\) be Representation category of affine Group scheme \(G\). And let \({\rm For}: \cat{Rep}_{k}(G) \to \cat{Vec}_{k}\) be forgetful functor. Then we have \(\cat{Aut}^{\otimes}({\rm For})( R) \ni \lambda\) is data of \(\lambda_{X}: X \otimes R \to X \otimes R\) for every \(X \in \cat{Rep}_{k}(G)\) with compatibilities
- \(\lambda_{X_{1} \otimes X_{2}} = \lambda_{X_{1}} \otimes \lambda_{X_{2}}\)
- \(\lambda_{\bold 1} = \id_{k \otimes R = R}\)
And for all \(\alpha: X \to Y\) in \(\cat{Rep}_{k}(G)\), it commutes with \(\lambda_{X}\). We observe that \(g \in G( R)\) gives an element of \(\cat{Aut}^{\otimes}({\rm For})( R)\). In fact, we have
The associated morphism of schemes \(G \to \cat{Aut}^{\otimes}({\rm For})\) is an isomorphism.
Representation category
For a group \(G\), we may define the category \(\cat{Rep}(G)\) for finite dimensional representation of \(G\) with morphisms of representations.
Cf. Algebraic group.
Referenced: Reconstruction theorem.
Representation of finite groups
A representation of a group \(G\) is homomorphism \(\phi: G \to GL(V)\) for some (finite-dimensional) vector space \(V\). The dimension of \(V\) is called the degree of \(\phi\).
equivalence; G-invariant subspace; irreducible representation; completely reducible representation; indecomposable representation; unitary representation
Schur lemma
Let \(\phi\), \(\rho\) be irreducible representation of \(G\), and \(T \in \Hom_{G}(\phi, \rho)\). Then either \(T\) is invertible or \(T = 0\).
Let \(G\) be an abelian group. Then any irreducible representation of \(G\) has degree 1.
Tensor product of irreducible representations
TODO Dykin diagram
Linear Algebra
Simultaneously diagonalizable
For two linear endomorphism \(A, B\), if \([A,B] = 0\), then \(A, B\) can be simultaneously diagonalized.
Lie Algebra
Base
A base of a Root system \(\Delta \in \phi\) is a basis for \(V\) such that each \(\alpha \in \phi\) is a positive or negative integer linear combination from \(\Delta\).
For a base \(\Delta\) we have \(\NN \Delta \cap \phi\) system of Positive roots. And positive roots can give a bases by simple roots.
Referenced: Fundamental weight.
Dominant
For \(\{\lambda_{i}\}\) Fundamental weights, \(\lambda \in P(\phi) = \oplus_{i} \ZZ \lambda_{i}\) is called dominant if \(\langle \lambda, \alpha_{j}^{\vee} \rangle \geq 0\) for all \(j\).
Cf. Root system.
Fundamental weight
For \(\Delta = \{\alpha_{1}, \cdots, \alpha_{n}\}\) Base for \(\phi\), we define the fundamental weights \(\{\lambda_{1}, \cdots, \lambda_{n}\}\) basis for \(V\) dual to \(\Delta^{\vee}\) so that \(\langle \lambda_{i}, \alpha_{j}^{\vee}\rangle = \delta_{ij}\).
Cf. Root system.
Referenced: Dominant.
TODO Poinccaré-Birkhoff-Witt theorem
Positive root
Let \((G, T)\) split Reductive, there exists Borel \(B \supset T\), and therefore \(\mathfrak{b} \supset \mathfrak{t}\). Let \(\phi\) be the Root system of \(G\), we define the positive root to by \(\phi^{+ }(B) = \{\alpha \in \phi \mid \mathfrak{g}_{\alpha} \subset \mathfrak{b}\}\).
Referenced: Base.
TODO Root system
Referenced: Base, Dominant, Fundamental weight, Positive root.
TODO simple root
Referenced: Base.
Differential Geometry
Cartan’s magic formula
On a smooth manifold \(M\) for any smooth vector field \(V\) and any smooth differential form \(\omega\), \[\mathscr{L}_{V} \omega = V \iprod (\dif \omega) + \dif (V \iprod \omega)\]
Collar
A collar of a smooth boundary Manifold \(M\) is a diffeomorphism \(\kappa: \partial M \times \rinterval{0}{1} \to M\) where the image is an open neighborhood of \(\partial M\) in \(M\) and \(\kappa(x, 0) = x\).
For collar, we have following proposition
A smooth boundary manifold \(M\) has a collar.
The proposition is similar to the existence of the tubular neighborhood for Normal bundle.
Complete integral distribution
Given a rank \(k\) Distribution \(D \subset TM\), let us say that a smooth coordinate chart \((U, \phi)\) on \(M\) is flat for \(D\) if \(\phi(U)\) is a cube in \(\RR^{n}\) and at points of \(U\), \(D\) is spanned by the first \(k\) coordinate vector fields \(\partial/ \partial x^{1}, \cdots, \partial/ \partial x^{k}\).
A distribution \(D \subset TM\) is completely integrable if there exists a flat chart for \(D\) in a neighborhood of each point of \(M\).
Referenced: Frobenius theorem.
Connected sum
Given two \(n\)-manifolds \(M_{1}\), and \(M_{2}\), we define the connected sum of \(M_{1}\) and \(M_{2}\) by remove two \(D^{n}\) in \(M_{1}\) and \(M_{2}\) and glue two \(S^{n - 1}\) together, denoted by \(M_{1} \shar M_{2}\).
Connection
A connection on a Vector bundle \(E \to M\) is a linear map \(\nabla^{E} : C^{\infty}(E) \to C^{\infty}(E \otimes T^{ *}M)\) satisfying the condition \[\nabla^{E}(\alpha e) = \alpha \nabla^{E} e + e \otimes \dif \alpha\] whenever \(e \in C^{\infty}\) is a smooth section of \(E\) and \(\alpha\) is a smooth function on \(M\).
A connection on a Principal bundle is a linear map \(A: TP \to \ker(\pi_{*})\) that equals the identity on the kernal of \(\pi_{*}\) and is equivariant with respect to the action of \(G\) on \(P\). Here \(\pi: P \to M\) is the projection map, \(\ker(\pi_{*})\) is often called vertical subbundle. Equivariant means that if \(g \in G\) and \(v \in TP\), then \((m_{g})_{*} (Av) = A((m_{g})_{*} v)\). \(\ker(A)\) is often called horizontal subbundle.
By isomorphism of \(\psi: P \times \mathfrak{lie}(G) \to \ker(\pi_{*})\) we can view a connection as a map \[A: TP \to \mathfrak{lie}(G)\] (or in other words \(A: \mathfrak{lie}(G) \to \mathfrak{lie}(G) \times T^{*}M\)) with \(A(\psi(p,m)) = m\) and \(A(m_{g*}v) = gA(v)g^{-1}\)
Referenced: Flat, Covariant derivative, Curvature, Holonomy group, Horizontal subbundle, Vertical subbunel, Chern class, Chern-Simons functional.
Flat
A Connection is called flat if the Curvature of the connection is identically zero.
Referenced: Chern-Simons functional.
Covariant derivative
The covariant derivative for Vector bundle is same as Connection. (Not sure)
Given a connection on a Principal bundle \(P\), we defines a covariant derivative \(\nabla_{A}\) on \(P \times_{\rho} V\) where \(\rho\) is a representation of \(G\) on \(V\). The Horizontal subbundle \(H_{A} \subset TP\) is canonically isomorphic to \(\pi^{*}TM\). For section \(s\) of \(E\), we can view it as \(G\)-equivariant map \(s^{P}:P \to V\). Then the restriction to \(H_{A}\) of the homomorphism \((s^{P})_{*}: TP \to V\) defines a covariant derivative of \(s\). In other word, let \(x \in M\) and \(v \in TM|_{x}\). Pick \(p \in P|_{X}\), then there exists a unique \(v_{A} \in H_{A}|_{p}\) such that \(\pi_{*} v_{A} = v\). Then \(\nabla_{A}s\) defined to send \(v\) to the equivalence class in \(E|_{x} = (P|_{x} \times_{\rho} V)\) of the pair \((p, (s^{p})_{*}v_{A})\).
Referenced: Exterior covarint derivative.
Curvature
For a given Connection and therefore Exterior covarint derivative \(\nabla^{E}\), there exists a unique smooth section \(R(\nabla^{E}) \in C^{\infty}(\End(E) \otimes \wedge^{2} T^{* }M)\) called the curvature of \(\nabla^{E}\), that satisfies the equation \[R(\nabla^{E}) \cdot (e \otimes v \wedge w) = \nabla_{v}^{E} \nabla_{w}^{E} e - \nabla_{w}^{E} \nabla_{v}^{E} e - \nabla^{E}_{ [v,w]}e\] for all \(v,w \in C^{\infty}( TM)\) and \(e \in C^{\infty}(E)\).
Or we can define curvature \(F_{\nabla}\) by \(\dif_{\nabla}^{2}m = F_{\nabla} \wedge m\).
The famous Bianchi identity is \[\dif_{\nabla} F_{\nabla} = 0\]
For Principal bundle, we define the \(F_{A}\) to be the section of the bundle \((P \times_{ad} \mathfrak{lie}(G)) \otimes \wedge^{2} T^{*}M\).
Referenced: Flat, Chern class, Chern-Simons functional, Yang-Mills equation.
Degree
Suppose \(M\) and \(N\) are compact, connected, Oriented, smooth manifolds of dimension \(n\), and \(F: M \to N\) is a smooth map. There exists a unique integer \(k\) called the degree of \(F\), that satisfies
- For every smooth \(n\)-form \(\omega\) on \(N\) \[\int_{M} F^{* } \omega = k \int_{N} \omega\]
- If \(q\) is a Regular value of \(F\), then \[k = \sum_{x \in F^{-1}(q)} \sgn(x)\] where \(\sgn(x) = 1\) if \(\dif F_{x}\) is orientation-preserving and \(-1\) if orientation-reversing.
de Rham cohomology
We define the de Rham cohomology group in degree \(p\) to be the quotient vector space \[H_{dR}^{p}(M) = \frac{Z^{p}(M)}{B^{p}(M)}\] where \(Z^{p}(M)\) is the closed \(p\)-forms on \(M\). then \(B^{p}(M)\) is the exact \(p\)-forms.
The de Rham cohomology is homotopy invariants. If \(M\) and \(N\) is homotopy equivalent manifolds, then \(H_{dR}^{n}(M) \cong H^{p}_{dR}(N)\) for each \(p\). The isomorphisms are induced by any smooth homotopy equivalence \(F: M \to N\).
Referenced: de Rham theorem, Cohomology.
de Rham theorem
For every smooth manifold \(M\) and nonnegative integer \(p\), the de Rham homomorphism \(J: H_{dR}^{p}(M) \to H^{p}(M; \RR)\) is an isomorphism.
Cf. Singular cohomology and de Rham cohomology.
Differential form
A section of \(\Lambda^{k}T^{* }M\) is called a differential \(k\)-form. The integer \(k\) is called the degree of the form.
Cf. Tangent bundle.
Referenced: Exterior derivative, Invariant formula for the exterior derivative, Stokes’s theorem.
Distribution
Cf. Tangent bundle.
A distribution on \(M\) of rank \(k\) is a rank \(k\) subbundle of \(TM\). It is called a smooth distribution if it is a smooth subbundle.
Referenced: Complete integral distribution, Integral distribution, Involutive distribution.
Exterior derivative
We define the exterior differential of Differential form \[\dif (\sum_{J} \omega_{J} \dif x^{J}) = \sum_{J} \dif \omega_{J} \wedge \dif x^{J}\]
Referenced: Exterior covarint derivative, Invariant formula for the exterior derivative, Stokes’s theorem.
Exterior covarint derivative
Cf. Exterior derivative.
Given a Covariant derivative \(\nabla\), we can define the exterior covariant derivative to be \(\dif_{\nabla}\) such that if \(\omega\) is a \(p\) form and \(s\) is a section of \(E\), then \(\dif_{\nabla}(s \omega) = \nabla(s) \wedge \omega + s \dif \omega\)
Referenced: Curvature.
Frobenius theorem
By definition, we have Complete integral distribution implies Integral distribution and integral distribution implies Involutive distribution. The Frobenius theorem suggests the reverse.
Every involutive distribution is completely integrable.
Holonomy group
Let \(M\) be a Manifold, \(E\) a Vector bundle over \(M\), and \(\nabla^{E}\) a Connection on \(E\). Suppose \(\gamma: [0,1] \to M\) is smooth, with \(\gamma(0) = x\) and \(\gamma(1) = y\), where \(x,y \in M\). Then for each \(e \in E_{x}\) there exists a unique smooth section \(s\) of \(\gamma^{* }(E)\) satisfying \(\nabla_{\dot{\gamma}(t)}^{E} s(t) = 0\) for \(t \in [0,1]\) with \(s(0) = e\). Define \(P_{\gamma}(e) = s(1)\). Then \(P_{\gamma}: E_{x} \to E_{y}\) is a well-defined linear map called the parallel transport map.
Fix a point \(x \in M\), we define the holonomy group \(\hol_{x}(\nabla^{E}) = \{P_{\gamma}: \gamma \text{ is a loop based at } x\} \subset \GL(E_{x})\).
Referenced: Kähler manifold with holomorphic symplectic structure.
Berger classification theorem
Suppose \(M\) is a simply connected manifold of dimension \(n\) and \(g\) is irreducible, nonsymmetric Riemannian metric on \(M\). Then exactly one of the following seven cases holds:
- \(\hol(g) = \SO(n)\).
- \(n = 2m\) with \(m \geq 2\), and \(\hol(g) = \U(m) \subset \SO(2m)\).
- \(n = 2m\) with \(m \geq 2\), and \(\hol(g) = \SU(m) \subset \SO(2m)\).
- \(n = 4m\) with \(m \geq 2\), and \(\hol(g) = \Sp(m) \subset \SO(4m)\).
- \(n = 4m\) with \(m \geq 2\), and \(\hol(g) = \Sp(m) \Sp(1) \subset \SO(4m)\).
- \(n = 7\) and \(\hol(g) = G_{2} \subset \SO(7)\).
- \(n = 8\) and \(\hol(g) = \Spin(7) \subset \SO(8)\).
Horizontal subbundle
See Connection.
Referenced: Covariant derivative.
Immersion
A smooth map \(f\) is an immersion if each \(T_{x}f\) is injective and submersion if each \(T_{x}f\) is surjective. Cf. Tangent space.
Referenced: Normal bundle, Submersion, Knot, Link.
Integral distribution
A nonempty immersed submanifold \(N \subset M\) is called an integral manifold of \(D\) if \(T_{p}N = D_{p}\) at each point \(p \in N\). And a Distribution is called integral if every point of \(M\) is contained in an integral manifold.
Referenced: Frobenius theorem.
Invariant formula for the exterior derivative
Let \(M\) be a smooth Manifold, and \(\omega \in \Omega^{k}(M)\). For any smooth vector fields \(X_{1}, \cdots, X_{k + 1}\) on \(M\).
\begin{align}\dif \omega (X_{1}, \cdots, X_{k + 1}) &= \\ & \sum_{1 \leq i \leq k + 1}(-1)^{i - 1}X_{i}(\omega(X_{1}, \cdots, \widehat{X_{i}}, \cdots, X_{k + 1})) \\ & + \sum_{1 \leq i < j \leq k + 1} (-1)^{i + j} \omega([X_{i}, X_{j}], X_{1}, \cdots, \widehat{X}_{i}, \cdots, \widehat{X_{j}}, \cdots, X_{k + 1}) \end{align}
Cf. Differential form, Exterior derivative.
Involutive distribution
The Distribution \(D\) is involutive if given a pair of smooth local sections of \(D\), their Lie bracket is also local section of \(D\).
Referenced: Frobenius theorem.
Lie derivative
Given a smooth covariant tensor field \(A\) on \(M\), we define the Lie derivative of \(A\) with respect to \(V\), denoted by \(\mathscr{L}_{V}A\) by \[(\mathscr{L}_{V}A)_{p} = \frac{\dif}{\dif t} \mid_{t = 0} (\theta_{t}^{* }A)_{p}\] Here \(V\) is a smooth vector field on \(M\), and \(\theta\) is its flow. \(\theta_{t}\) is locally an isomorphism.
Referenced: Liouville vector field.
Lie group
A Lie group is a smooth manifold with a group structure, where the group multiplication and inverse are smooth maps.
Cf. Manifold.
Referenced: Principal bundle.
TODO E8
Referenced: Intersection forms.
Manifold
An \(n\)-dimensional manifold is an \(n\)-dimensional locally Euclidean Hausdorff space with countable basis for its topology.
The definition has three requirements, where the countable basis is hardly used.
A differential structure on the \(n\)-manifold \(M\) is a maximal smooth atlas \(\mathscr{D}\) for \(M\). The pair \((M, \mathscr{D})\) is called a smooth manifold or differentiable manifold.
We call a compact manifold without boundary a closed manifold.
Referenced: Collar, Connected sum, Holonomy group, Invariant formula for the exterior derivative, Lie group, Orientation, Riemannian metric, Tangent space, Whitney embedding theorem, Fundamental class, Local homology group, Poincaré duality, Symplectic manifold, Freedman’s classification of topological 4-manifold, Rokhlin Theorem, Spin structure.
Normal bundle
Let \(f: M \to N\) be an Immersion. We define the quotient bundle of the bundle morphism \(i: TM \to f^{* }TN|_{M}\) to be the normal bundle. There exists a neighborhood of the zero section of normal bundle diffeomorphic to the neighborhood of \(N\) in \(M\). The diffeomorphic map is called tubular map and the target is called tubular neighborhood.
Cf. Vector bundle, Tangent bundle.
Referenced: Collar.
Orientable
See Orientation.
Referenced: Heegaard diagram, Trisection.
Orientation
An atlas is called orienting if any two charts are positively related, that is every two charts has the same orientation as a subset of \(\RR^{n}\). If a Manifold \(M\) has an orienting atlas, we call \(M\) orientable. Notice that if a manifold is orientable, it naturally has two orientation.
Given Local homology group, a generator of the homology group \(H_{n}(M, M \backslash x; R) \cong R\) is called a local \(R\)-orientation. Let \(M\) be a \(n\)-manifold and \(A \subset M\). An \(R\)-orientation of \(M\) along \(A\) is a section \(s \subset \Gamma(A; R)\) of \(\omega: H_{n}(M, M \backslash \bullet; R) \to M\) such that \(s(a) \in H_{n}(M, M \backslash a; R) \cong R\) is a generator for each \(a \in A\). For \(A = M\), we called it \(R\)-orientation and for \(R = \ZZ\), it is called orientation.
By characteristic class theory, a manifold is orientable if the first Stiefel-Whitney class vanishes that is \(w_{1}(E) = 0\).
Referenced: Degree, Orientable, Oriented, Euler class, Fundamental class, Poincaré duality, Lickorish-Wallace theorem.
Oriented
See Orientation.
Referenced: Linking number, Seiberg-Witten moduli space, Seifert surface, Trisection.
Poincaré lemma
If \(U\) is a star-shaped open subset of \(\RR^{n}\) of \(\HH^{n}\), then every closed covector field on \(U\) is exact.
Principal bundle
A principal bundle is a fiber bundle with fiber Lie group \(G\) and free \(G\) actions fiberwise.
Referenced: Connection, Covariant derivative, Curvature.
Regular point
For a smooth map \(f: M \to N\), a point \(x \in M\) is called a regular point if \(T_{x}f\) is surjective and a point \(y \in N\) is called a regular value if each \(x \in f^{-1}(y)\) is a regular point, otherwise is called a singular value. Cf. Tangent space.
Referenced: Degree, Sard theorem, Critical point.
Riemannian metric
A Riemannian metric on \(M\) is a smooth symmetric covariant \(2\)-tensor field on \(M\) that is positive definite at each point. A Riemannian manifold is a pair \((M, g)\), where \(M\) is a smooth manifold and \(g\) is a Riemannian metric on \(M\).
Cf. Manifold.
Every smooth manifold admits a Riemannian metric.
By Numerable property of the smooth manifold.
Referenced: Spin^C connection.
Sard theorem
The set of singular values of a smooth map has measure zero, and the set of regular values is dense.
Cf. Regular point.
In most applications, the dense property implies the existence, as in the case of Whitney embedding theorem.
Referenced: Whitney embedding theorem, Seiberg-Witten moduli space.
Stein manifold
A stein manifold is a complex manifold which is a holomoprhically convex and holomorphically separable subset of \(\CC^{n}\). This is equivalent to \(\Sigma\) admits a proper holomorphic immersion \(\Sigma \hookrightarrow \CC^{n}\). In particular, analytification of any affine variety over \(\CC\) is a Stein space, but the converse is not true.
Stokes’s theorem
Let \(M\) be an oriented smooth \(n\)-manifold with boundary, and let \(\omega\) be a compactly generated supported smooth \((n - 1)\)-form on \(M\). Then \[\int_{M} \dif \omega = \int_{\partial M} \omega\]
Cf. Differential form, Exterior derivative.
Submersion
See Immersion.
Tangent bundle
The Tangent space at each point constitutes a Vector bundle called the tangent bundle.
Referenced: Differential form, Distribution, Normal bundle.
Tangent space
We denote the tangent space at point \(p\) by \(T_{p}(M)\), and to each map \(f: M \to N\) associated a linear map \(T_{p}(f): T_{p}(M) \to T_{f(p)}N\) the differential of \(f\) at \(p\), such that \[T_{p}(gf) = T_{f(p)} g \circ T_{p}f\] The elements of \(T_{p}(M)\) are the tangent vectors of \(M\) at \(p\). Cf. Manifold.
Referenced: Immersion, Regular point, Tangent bundle, Predeformation functor.
TODO Uhlenbeck compactification
Vertical subbunel
See Connection.
Wedge product
For \(w \in \Lambda^{k}(V^{* })\) and \(\eta \in \Lambda^{l}(V^{* })\), we define the wedge product or exterior product to be \[\omega \wedge \eta = \frac{(k+l)!}{k!l!} {\rm Alt}(\omega \otimes \eta)\]
Whitney embedding theorem
A smooth \(n\)-manifold has an embedding as a closed submanifold of \(\RR^{2n + 1}\).
Cf. Sard theorem, Manifold.
Algebraic Topology
Alexander-Whitney map
Referenced: Cup product.
Base
See Fibre bundle.
Borsuk-Ulam theorem
Let \(f: S^{2} \to \RR^{2}\). Then there exists \(x \in S^{2}\) such that \(f(x) = f(-x)\).
Cf. Degree.
Bott periodicity
We consider the Grothendieck ring of vector bundles. We have that
\(K(S^{2})\) is free abelian group with basis \(1\) and \(\eta = H(1)\). The multiplicative structure is determined by \(\eta^{2} = 2 \eta - 1\).
Cf. Complex line bundle over CP^1.
The Bott periodicity is the following deep result
\[K(X) \otimes K(S^{2}) \cong K(X \times S^{2})\] \[KO(X) \otimes KO(S^{8}) \cong KO(X \times S^{8})\]
Brouwer fixed point theorem
The Brouwer fixed point theorem is an example of non construction existence proof.
Let \(f: D^{2} \to D^{2}\). Then there exists \(x \in D^{2}\) such that \(f(x) = x\).
The Brouwer fixed point theorem can give a proof of the fundamental theorem of algebra.
Referenced: Existence proof.
Category CGWH
denote the full subcategory of Compactly generated Weak Hausdorff space by \(\cat{CGWH}\).
The category \(\cat{CGWH}\) is complete and cocomplete.
Cf. Complete, Cocomplete.
Also, we have for \(X, Y \in \cat{CGWH}\), \[{\rm Map}(X, Y) \in \cat{CGWH}\] and the exponential law holds.
Referenced: Realization, Loop space.
Cellular
Let \((X, Y)\) be CW complexes. A map \(f: X \to Y\) is called cellular if \(f(X^{n}) \subset Y^{n}\) for any \(n\). We define the category \((cat{CW})\) whose objects are CW complexes and morphisms are cellular maps.
Referenced: Cellular approxiamtion theorem, Cellular homotopy.
Cellular approxiamtion theorem
Any map between relative CW complexes is homotopic to a cellular map. If two cellular maps between relative CW complexes are homotopic, then they are cellular homotopic.
Cf. Cellular homotopy, Cellular and Relative CW complex.
Cellular homotopy
A cellular homotopy between two Cellular maps \(X \to Y\) is a Homotopy \(X \times I \to Y\) that itself a cellular map. The quotient category is called \(\cat{hCW}\).
Referenced: Cellular approxiamtion theorem.
Chern class
Consider complex Vector bundle \(E \to X\), we wan to find sections linear independent everywhere. Then we have primary obstruction Chern class \(c_{n - k + 1} \in H^{2 (n - k + 1)}(X; \ZZ)\). Axioms of Chern class include \(c_{0}(E) = 1\), naturality and product structure and normalization \(c(T \CC \PP^{n}) = (1 + w)^{n + 1}\) for \(w = \pd [\CC \PP^{n - 1}]\).
All characteristic class (classes satisfies the naturality condition) for complex vector bundles are combination of Chern classes.
For complex manifod, with Connection \(\nabla_{A}\), we can calculate the Chern class analytically by Chern-Weil formula
\[\sum t^{k}c_{k}(E) = \det(I - \frac{t F_{A}}{2 \pi i})\] where \(F_{A}\) is the curvature with respect to connection \(\nabla_{A}\).
Cf. Curvature.
This can be generalized to principal bundles.
Referenced: Pontryagin class, Chern-Weil theory.
Classifying Space
We consider the functor \(B(-, G)\) from the category of topological space to sets, where \(B(B,G)\) denote the set of isomorphism classes of Numerable \(G\) principal bundles over \(B\). We have that functor representable by classifying space \(BG\), with a numerable \(EG \to BG\). The total space \(EG\) is called universal if each numerable free \(G\) space \(E\) has up to \(G\)-map \(E \to EG\).
We can construct \(EG, BG\) by join. We consider a family of topological space \(X_{j} \in J\). Then we have \[X = \star_{j \in J} X_{j} = \{(t_{i}X_{i})_{i \in J}| \sum_{i \in J}t_{i} = 1\}/ \sim\] where the summation has finite nonzero summand \((t_{i}X_{i}) \sim (s_{i}Y_{i})\) if \(t_{i} = s_{i}\) and \(X_{i} = Y_{i}\) when \(t_{i} = s_{i} \neq 0\). The topology of the space \(X\) is the coarsest topology where the function \(t_{i}: X \to \mathbb{R}, (t_{i}X_{i}) \to t_{i}\) and function \(t_{i}:t_{i}^{-1}(\linterval{0}{1}) \to X_{i}, (t_{i}X_{i}) \to X_{i}\) is continuous.
Then we construct the Milnor space \[EG = G \star G \star G \star \cdots\] and \(BG = EG/G\). The action of \(G\) is obvious.
\(EG\) is contractible.
For a discrete group, \(BG\) is an Eilenberg-Mac Lane space of type \(K(G,1)\).
Cobordism hypothesis
Cofibered
We say a pair \((X, A)\) is cofibered if the inclusion \(A \subset X\) is a Cofibration.
Cofiber exact sequence
Cf. Exact Puppe sequence. Let \(f: X \to Y\) in \(\cat{CGWH*}\) between well-pointed spaces. The following sequence is co-exact in \(\cat{hCGWH*}\) \[X \to Y \to C_{* f} \to \Sigma X \to \Sigma Y \to \Sigma C_{* f} \to \Sigma^{2}X \to \cdots\] Cf. Cone.
Cofibration
A map \(i: A \to X\) is called a cofibration if it has Homotopy extension property for any spaces.
An equivalent saying is the follow one.
Let \(i: A \to X\) and \(j: M_{i} \to X \times I\). Then \(i\) is a cofibration if and only if there exists \(r: X \times I \to M_{i}\) such that \(r \circ j = 1_{M_{i}}\).
Let \(i: A \to X\) be a cofibration. Then \(i\) is a homeomorphism to its image. If we work in \(\cat{CGWH}\), then \(i\) has closed image.
The inclusion \(S^{n - 1} \to D^{n}\) is a cofibration.
Referenced: Cofibered, Well-pointed.
Cohomology
There are various cohomology theories. The can be defined by common axioms.
A cohomology theory for pairs of spaces with values in the category of \(R\)-modules consists of a family \((h^{n} \mid n \in \ZZ)\) of contravariant functors \(h^{n}: TOP(2) \to R-MOD\) and natural transformations \(\delta^{n}: h^{n - 1} \circ \kappa \to h^{n}\) such that
- Homotopy invariance. Homotopic maps \(f_{0}\) and \(f_{1}\) between pairs of space induces the same homomorphism \(h^{n}(f_{0}) = h^{n}(f_{1})\).
- Exact sequence. For each pair \((X, A)\), we have exact sequence \[\cdots \to h^{n - 1}(A, \emptyset) \stackrel{\delta}{\to} h^{n}(X, A) \to h^{n}(X, \emptyset) \to h^{n}(A) \to \cdots \]
- Excision. Let \((X, A)\) be a pair and \(U \subset A\) such that \(\bar{U} \subset A^{\circ}\). Then the inclusion \((X \backslash U, A \backslash U) \to (X,A)\) induces an isomorphism \(h^{n}(X, A) \cong h^{n}(X \backslash U, A \backslash U)\).
Cf. Excision theorem, Mayer-Vietoris sequence.
Given a cohomology theory, we called \(h^{n}(X,A)\) the \(n\)-th cohomology group. The \(\delta^{n}\) are called the coboundary operator. And we write \(h^{n}(X) := h^{n}(X, \emptyset)\).
As in homology theory, we called \(h^{n}(pt)\) the coefficient groups of the theory and a cohomology theory may have following additional axioms
- dimension axiom. \(h^{n}(pt) = 0\) for \(n \neq 0\).
- additive axiom. \[h^{n}(\coprod X_{j}, \coprod A_{j}) \to \coprod_{j} h^{n}(X_{j}, A_{j})\] is always an isomorphism.
Also, we have triple exact sequence \[ \cdots \to h^{n - 1}(A, B) \stackrel{\delta}{\to} h^{n}(X, A) \to h^{n}(X, B) \to h^{n}(A, B) \stackrel{\delta}{\to} \cdots\]
Cf. de Rham cohomology.
Referenced: Cap product, Eilenberg-Mac Lane space, Excision theorem, Mayer-Vietoris sequence, Reduced cohomology, Category of modules.
Singular cohomology
Cf. Singular homology.
We consider the cochain complex \(S^{n}(X; G) = \Hom(S_{n}(X), G)\) and define the i-th singular cohomology by the i-th cohomology group of the cochain complex.
Referenced: de Rham theorem.
Relative singular cohomology
We define the relative singular cochain complex by \(S^{\bullet}(X, A; G) = \Hom(S_{\bullet}(X)/S_{\bullet}(A), G)\). Its cohomology is called the relative singular cohomology.
Compactly supported cohomology
Let \(\mathscr{K}\) denote the set of compact subspaces of \(X\). We define compactly supported cohomology of \(X\) by \[H_{c}^{k}(X) :=\colim_{K \in \mathscr{K}} H^{k}(X, X - K)\] In particular if \(X\) is compact, we have \(H_{c}^{k}(X) = H^{k}(X)\).
The compactly supported cohomology also satisfies Mayer-Vietoris sequence.
Referenced: Poincaré duality.
Cup product
One of the most difference between homology theory and cohomology theory is the multiplicative structure making cohomology group a cohomology rings. \[h^{m}(X, A) \otimes_{R} h^{n}(X, B) \to h^{m + n}(X, A \cap B)\] We call \(x \cap y\) the cup product of \(x, y\). The cup product is defined if \(A\) or \(B\) is empty or \(A = B\). We have axioms of cup product
- Naturality: For triads \(f:(X, A, B) \to (X'; A', B')\) we have \[f^{ *}(x \cup y) = f^{ *}(x) \cup f^{ *}(y)\]
- Stability: TODO
- Unit element: There is a unit \(1 \in h^{0}(pt)\) such that \(1_{X} = p^{*}(1)\) is the unit of multiplication in cohomology ring.
- Associativity: \((x \cup y) \cup z = x \cup (y \cup z)\).
- Commutativity: \(x \cup y = (-1)^{\abs{x} \abs{y}} y \cup x\). Here \(\abs{x}\) is the grade in the cohomology ring.
For the most importanct case \(A = B = \emptyset\), the cup product can be given by Alexander-Whitney map, that is \[(\alpha \cup \beta)(\sigma) = \alpha(_{p}\sigma) \cdot \beta(\sigma_{q})\]
The morphism \(H^{* }(-; R)\) is natural, that is it is a functor from the category of topological spaces to the category of graded commutative rings.
Cap product
We have cap product between Cohomology and Homology. That is we first consider the pairing \[\langle -, - \rangle: S^{\bullet}(X; R) \times_{R} S_{\bullet}(X;R) \to R\] for \(\alpha \in S^{p}(X)\), \(\sigma \in S_{p}(X)\), \(r \in R\), defined as \(\langle \alpha, (\sigma \otimes r) \rangle = \alpha(\sigma) \cdot r\).
The we define the cap product by composing the above pairing by \(1 \otimes \Delta\), so we have \[S^{\bullet}(X;R) \otimes S_{\bullet}(X;R) \to S^{\bullet}(X;R) \otimes S_{\bullet}(X \times X; R) \to S^{\bullet}(X;R) \otimes S_{\bullet}(X;R) \otimes S_{\bullet}(X;R) \to S_{\bullet}(X;R)\] which induced the map \[\cap : H^{p}(X; R) \otimes H_{p + q}(X; R) \to H_{q}(X; R)\]
The cap product makes \(H_{\bullet}(X; R)\) an \(H^{\bullet}(X;R)\)-module.
The cap product can be generalized to relative case \[\cap: H^{p}(X;A) \otimes H_{p + q}(X, A) \to H_{q}(X)\] \[\cap: H^{p}(X) \otimes H_{p + q}(X, A) \to H_{q}(X, A)\]
External product
For details see, section 17.3 in [dieck2008].
The external product is a family of \(R\)-linear maps \[h^{m}(X, A) \otimes_{R} h^{n}(Y, B) \to h^{m + n}((X, A) \times (Y, B)), x \otimes y \to x \times y\] The external products satisfying some properties.
Compactly generated
A subset \(Y \subset X\) is called compactly closed or \(k\)-closed if \(f^{-1}(Y)\) is closed in \(K\) for every continuous map \(f: K \to X\) with \(K\) compact Hausdorff. We define a new topology on \(X\) denoted by \(X\), where close subsets of \(kX\) are compactly closed subsets of \(X\). The map \(kX \to X\) is a continuous map. \(X\) is called compactly generated if \(kX = X\). The full subcategory of \(\cat{Top}\) consisting of compactly generated space is denoted by \(\cat{CG}\).
Every locally compact Hausdorff space is compact generated.
We have exponential law in \(\cat{CG}\).
Let \(X,Y,Z \in \cat{CG}\). Then we have homeomorphism \[{\rm Map}(X \times Y, Z) \to {\rm Map}(X, {\rm Map}(Y,Z))\]
Referenced: Category CGWH.
Complex line bundle over CP^1
We have that \(H(k) = (\mathbb{C}^{2} \backslash 0) \times_{\mathbb{C}^{* }} \mathbb{C}\) with equivalence relation \(((z_{0}, z_{1}), u) \sim ((\lambda z_{0}, \lambda z_{1}), \lambda^{k} u) \). Then we have that \(H(k)\) represent the isomorphism classes of complex line bundles.
This is a simple but non-trivial fact, leading naturally to the problems of complex line bundles over \(\mathbb{C}P^{n}\). And more generally, vector bundles over \(\mathbb{C}P^{n}\).
Cf. Vector bundle
Referenced: Bott periodicity.
Cone
Let \((X, x_{0}) \in \cat{CGWH*}\). We define its cone by \[C_{* }X = X \wedge I = X \times I / (X \times \{0\} \cap \{x_{0}\} \times I)\] Cf. Smash product.
Referenced: Cofiber exact sequence, Homotopy cofiber.
TODO Contractible
Referenced: Integer homology 3-sphere.
Covering
A covering (space) is a Locally trivial map \(p: E \to B\) with discrete Fibre \(F\). A covering map which is a trivial Fibre bundle is also called a trivial covering.
\[S^{n} \to \RR P^{n}\] is a double covering.
The map \(\RR^{1} \to S^{1}\), \(t \to e^{2 \pi i t}\) is a \(\ZZ\)-covering.
Assume \(B\) is path connected, locally path connected and semi-locally simply connected and \(b \in B\). Then there exists an equivalence of categories \[\cat{Cov}(B) \cong \pi_{1}(B, b)-\cat{Set}\]
Cf. Path connected, Semi-locally simply connected.
Referenced: Deck transformation, Fibration, Fundamental group, G-principal covering, Lifting, Universal covering.
CW approximation
A CW approximation of a topological space \(Y\) is a CW complex \(X\) with a Weak homotopy equivalence \(f: X \to Y\).
The following theorem making the study of topological space reduces to the study of CW complex up to weak homotopy equivalence.
Any space has a CW approximation.
TODO CW complex
Referenced: Cellular, CW approximation, Eilenberg-Mac Lane space, Whitehead theorem.
Deck transformation
Let \(B\) be a Path connected and \(p: E \to B\) be a connected Covering. A deck transformation is a homeomorphism \(f: E \to E\) such that \(p \circ f = p\). We denote the group of deck transformations by \( \aut(p)\).
Deformation retract
See Retraction.
Referenced: Neighborhood deformation retract.
Degree
For degree of isogeny, see Isogeny.
For degree of a map \(f: S^{n} \to S^{n}\), the degree its image in the Homotopy group \(\pi_{n}(S^{n}) \cong \ZZ\).
Referenced: Borsuk-Ulam theorem.
Eilenberg-Mac Lane space
The Eilenberg-Mac Lane space \(K(G, n)\) is the space with homotopy group \(\pi_{i}(K(G,n)) = 0\) for \(i \neq n\) and \(G\) if \(i = n\).
The Eilenberg-Mac Lane spaces exist.
Eilenberg-Mac Lane space is the representation space for Cohomology, that is we have the following
\[H^{n}(X; G) \cong [X, K(G,n)]\] for any CW complex \(X\).
Cf. CW complex.
\[\CC P^{\infty} = K(\ZZ, 2)\]
Referenced: Classifying space, Classifying Space.
Eilenberg-Zilber theorem
If \(H_{0}(S_{\bullet}(X \times Y)) = H_{0}(S_{\bullet}(X)) \otimes H_{0}(S_{\bullet}(Y))\), then there exists natural transformations \[S_{\bullet}(- \times -) \stackrel{F}{\underset{G} \Longleftrightarrow} S_{\bullet}(-) \otimes S_{\bullet}(-)\] And therefore isomorphisms on homology groups. Here \(F\), \(G\) is called Eilenberg-Zilber map.
The proof of the theorem relies on Spectral sequence and is rather abstract. However, for Singular homology, there exists a explicit form of the Eilenberg-Zilber map, called Alexander-Whitney map. First for \(\sigma: \Delta^{n} \to X\), we introduce the map \( _{p} \sigma: \Delta^{p} \to X, _{p} \sigma(t_{0}, \cdots, t_{p}) = \sigma(t_{0}, \cdots, t_{p}, 0 ,\cdots, 0)\) and \(\sigma_{q}(t_{0}, \cdots, t_{q}) = \sigma(0, \cdots, 0, t_{0}, \cdots, t_{q})\), and then we have Alexander-Whitney map \[AW: S_{\bullet}(X \times Y) \to S_{\bullet}(X) \otimes S_{\bullet}(Y)\] given by \[AW(\sigma) = \sum_{p + q = n} {}_{p}(\pi_{X} \circ \sigma) \otimes (\pi_{Y} \circ \Sigma)_{q}\] By Eilenberg-Zilber theorem, the above map is a chain homotopy equivalence.
Cf. Homology.
Referenced: Alexander-Whitney map.
TODO Equivariant cohomology
Compared with classical cohomology theory, the equivariant cohomology is more general and simpler.
Referenced: Geometric representation theory.
TODO Equivariant K-theory
Referenced: Geometric representation theory.
Euler class
Let \(p: E \to X\) be a real Oriented Vector bundle of dimension \(n\), we want to find a nowhere vanishing section \(s: X \to E\), the primary obstruction is defined as the Euler class \(e(E) \in H^{n}(X; \ZZ)\). A geometric definition is taht we consider a generic section \(s: X \to E\) which is transverse to zero section, then \(s^{-1}(0)\) is a submanifold of \(X\) of codimension \(n\) and \(e(E)\) can be taken as Poincaré dual of \([s^{-1}(0)]\).
Referenced: Poincaré-Hopf thereom.
Exact Puppe sequence
A sequence in \(\cat{hCGWH}\) is exact if for any \(Y\), the sequence \(\cdots \to [Y, X_{n + 1}]_{0} \to [Y, X]_{0} \to [Y, X_{n - 1}]_{0} \to \cdots\) is exact. Let Homotopy fiber \(F_{f}\) be the pullback of \(p_{1}:P_{y_{0}}Y \to Y\) and \(f:X \to Y\) in category \(\cat{CGWH*}\). Then we have
The sequence \(F_{f} \overset{\pi}{\to} X \to \overset{f}{\to} Y\) is exact in \(\cat{hCGWH}\).
We also have that \(\Omega Y = F_{F_{f} \to X}\). So we have exact sequence
The sequence \(\Omega X \xrightarrow{\Omega f} \Omega Y \to F_{f} \xrightarrow{\pi} X \xrightarrow{f} Y\) is exact in \(\cat{hCGWH}\).
Also by considering the adjunction formula \([\sigma Y, X]_{0} = [Y, \Omega X]_{0}\), we have that
Let \(X_{1} \to X_{2} \to X_{3}\) be exact in \(\cat{hCGWH*}\), then so is \(\Omega X_{1} \to X_{2} \to X_{3}\).
Combining two lemmas above, we get the exact Puppe sequence
Let \(f:X \to Y\) in \(\cat{CGWH*}\). Then the following sequence is exact in \(\cat{hCGWH*}\). \[\cdots \to \Omega^{2}Y \to \Omega F_{f} \to \Omega X \to \Omega Y \to F_{f} \to X \to Y\]
Let \(p: E \to B\) be a fibration whose fiber over the base point is \(F\). Then we have an exact sequence of homotopy groups \[\cdots \to \pi_{n}(F) \to \pi_{n}(E) \to \pi_{n}(B) \to \pi_{n - 1}F \to \cdots \to \pi_{0}(E) \to \pi_{0}(B)\]
Cf. Fibration, Homotopy group.
Referenced: Cofiber exact sequence.
Excision theorem
The Mayer-Vietoris sequence has a equivalent description called excision theorem.
Let \(U \subset A \subset X\) be subspaces such that \(\bar{U} \subset A^{\circ}\). Then the inclusion \(i:(X - U, A - U) \to (X, A)\) induces isomorphisms \[i_{* }: H_{n}(X - U, A - U) \cong H_{n}(X, A), \; \forall n\]
Cf. Homology and Cohomology.
Referenced: Cohomology.
Fibration
A map \(p: E \to B\) is a fibration if \(p\) has Homotopy lifting property.
A covering is a fibration.
Cf. Covering.
By the corollary in Homotopy fiber, we see that fibration is similar to Fibre bundle. In the converse, we have following criterion for fibration
Let \(p:E \to B\) be a fiber bundle with \(B\) paracompact Hausdorff. Then \(p\) is a fibration.
Referenced: Kan fibration, Exact Puppe sequence, Homotopy fiber.
Fibre
See Fibre bundle.
Referenced: Covering.
Fibre bundle
Let \(p: E \to B\) be in \(\cat{Top}\). A trivialization of \(p\) over an open set \(U \subset B\) is a homeomorphism \(\phi:p^{-1}(U) \to U \times F\) over \(U\), such that the following diagram commutes
 \(p\) is called locally trivial if there exists an open cover \(\mathscr{U}\) of \(B\) such that \(p\) has trivialization over each open \(U \in \mathscr{U}\). Such \(p\) is called a fibre bundle, \(F\) is called the fiber and \(B\) is called the base. And we denoted by
\[F \to E \to B\]
\(p\) is called locally trivial if there exists an open cover \(\mathscr{U}\) of \(B\) such that \(p\) has trivialization over each open \(U \in \mathscr{U}\). Such \(p\) is called a fibre bundle, \(F\) is called the fiber and \(B\) is called the base. And we denoted by
\[F \to E \to B\]
Cf. Vector bundle.
\[S^{1} \to S^{2n + 1} \to \CC P^{n}\]
Referenced: Base, Covering, Fibration, Fibre, Homotopy fiber, Local trivial, Trvialization.
Fibre homotopy
For two fibrations \(p_{1}:E_{1} \to B\) and \(p_{2}: E_{2} \to B\) and two fiber maps \(f_{0}, f_{1}:p_{1} \to p_{2}\) are said to be fiber homotopic if there exists a homootpy \(F: E_{1} \times I \to E_{2}\) such that \(F(-, t)\) is a fiber map for each \(t \in I\). \(f:p_{1} \to p_{2}\) is a fiber homotopic equivalence if there exists an inverse.
Let \(p_{1}:E_{1} \to B\) and \(p_{2}: E_{2} \to B\) be two fibrations and \(f:E_{1} \to E_{2}\) be a fiber map. Assume \(f: E_{1} \to E_{2}\) is a homotopy equivalence, then \(f\) is a fiber homotopy equivalence. In particular, \(f: p_{1}^{-1}(b) \to p_{2}^{-1}(b)\) is a homotopy equivalence.
Fundamental class
Theorem 16.4.1 in [dieck2008].
Let \(M\) be a compact connected \(n\)-Manifold. Then one of the following holds:
- \(M\) is orientable, then we have that \(H_{n}(M) \cong \ZZ\) and for each \(x \in M\), \(r^{M}_{x}\) is isomorphism.
- \(M\) is non-orientable, then \(H_{n}(M) = 0\).
Cf. Orientation, Local homology group.
If \(M\) is orientable, then a generator will be called fundamental class. If \(M\) is a manifold with boundary, then we call \(z \in H_{n}(M, \partial M)\) a fundamental class if for each \(x \in M \backslash \partial M\) the restriction of \(z\) is a generator in \(H_{n}(M, M \backslash x)\), cf. Local homology group.
Theorem 16.5.1 (ibid.)
Let \(M\) be a compact connected \(n\)-manifold with non-empty boundary. Then one of the following holds:
- \(H_{n}(M, \partial M) \cong \ZZ\) and a generator of this group is a fundamental class. The image of the map \(\partial: H_{n}(M, \partial M) \to H_{n - 1}(\partial M)\) is a fundamental class. The interior \(M \backslash \partial M\) is orientable.
- \(H_{n}(M, \partial M) = 0\), and \(M \backslash \partial M\) is not orientable.
Referenced: Poincaré duality, Virtual fundamental class.
TODO Fundamental group
Let \(p: E \to B\) be a covering and \(E\) path connected. Let \(e \in E\) and \(b = p(e) \in B\). Then the action of \(\pi_{1}(B, b)\) on \(p^{-1}(b)\) is transitive, whose stabilizer at \(e\) is \(\pi_{1}(E, e)\). In other words, we have following exact sequence \[1 \to \pi_{1}(E, e) \to \pi_{1}(B, b) \to p^{-1}(b) \to 1\]
Cf. Covering.
Let \(p: E \to B\) be a \(G\)-principal covering, \(E\) path connected, \(e \in E\), \(b = p(e)\). Then we have an exact sequence of groups \[1 \to \pi_{1}(E, e) \to \pi_{1}(B, b) \to G \to 1\] That is \(\pi_{1}(E, e)\) is a normal subgroup of \(\pi_{1}(B, b)\).
Cf. G-principal covering and above theorem.
Referenced: Homotopy group, Seifert-Van Kampen theorem, Semi-locally simply connected, Braid group.
TODO Fundamental groupoid
Referenced: Seifert-Van Kampen theorem.
G-principal covering
A left \(G\)-principal covering is a Covering \(p: E \to B\) with a left Properly discontinuous \(G\)-action on \(E\) over \(B\) commutes with the covering map.
The map \(\RR^{1} \to S^{1}\) is a \(\ZZ\)-principal covering for action \(n: t \to t + n\).
Referenced: Fundamental group.
Grothendieck ring
Given a commutative monoid \(M\) which is a set together with an associative and commutative composition law \(+\) with zero element. We have a group \(K(M) = M \times M / D(M)\). That is elements of \(K(M)\) are of the form \((a,b) \in M \times M\), with equivalence relation \((a, b) \sim (c, d)\) if \((a + n, b + n) = (c + m, d + m)\) for some \(m,n \in M\). Such group is called Grothendieck group. If the monoid is given with a multiplicative structure, which can by inherited by Grothendieck group, the group becomes Grothendieck ring.
Referenced: Bott periodicity, Vector bundle.
TODO Homology
Referenced: Cap product, Eilenberg-Zilber theorem, Excision theorem, Hurewicz theorem, Whitehead theorem.
Singular homology
A singular n-simplex is a continuous map \(\sigma: \Delta^{n} \to X\), where \(\Delta^{n}\) is the Standard n-simplex. We define \(S_{n}(X)\) to be the free abelian group by all singular \(n\)-simplexes \(S_{n}(X) = \oplus_{\sigma \in \Hom(\Delta^{n}, X)} \ZZ \sigma\). An element of \(S_{n}\) is called a singular n-chain in \(X\). Given \(\sigma: \Delta^{n} \to X\), we have \(\partial^{i} \sigma: \Delta^{n - 1} \to X\) for \(0 \leq i \leq n\), by restricting the \(\sigma\) to the \(i\)-th face of the \(\Delta^{n}\) whose vertices are given by \(\{v_{0}, v_{1}, \cdots, \hat{v}_{i}, \cdots, v_{n}\}\). And we define the boundary map \(\partial: S_{n}(X) \to S_{n - 1}(X)\) to be \(\partial \sigma = \sum_{i = 0}^{n} (-1)^{i} \partial^{(i)} \sigma\). Then \((S_{\bullet}(X), \partial)\) defines a chain complex and we define the \(n\)-th singular homology group of \(X\) by \[H_{n}(X) = H_{n}(S_{\bullet}(X), \partial)\]
The singular homology groups are homotopy invariants.
The following theorem is sometimes called dimension axiom.
If \(X\) is contractible, then
\begin{equation} H_{n}(X) = \begin{cases} 0 & n > 0 \\ \ZZ & n = 0 \end{cases} \end{equation}
Referenced: Simplicial set, Singular cohomology, Eilenberg-Zilber theorem, Künneth formula, Local homology group, Poincaré duality.
Relative singular homology
Let \(A \subset X\) be a subspace. It induces a natural injective chain map \(S_{\bullet}(A) \to S_{\bullet}(X)\). We define the singular chain complex of \(X\) relative to \(A\) to be \[S_{n}(X, A) = S_{n}(X)/S_{n}(A)\] with the induced differential. Its homology \(H_{n}(X, A) = H_{n}(S_{\bullet}(X, A))\) is called the \(n\)-th relative homology.
TODO Reduced homology
Let \((X, x_{0})\) be a well-pointed space, then \(\tilde{H}_{n}(\Sigma X) = \tilde{H}_{n - 1}(X)\).
Cf. Suspension.
TODO Cellular homology
TODO Homotopy
Referenced: Simplicial homotopy, Cellular homotopy, Hurewicz theorem.
Homotopy cofiber
Cf. Homotopy fiber.
Given \(f: X \to Y\) in \(\cat{CGWH*}\), we define homotopy cofiber \(C_{ * f}\) by the push-out of \(X \to C_{*}X\) and \(f: X \to Y\). Cf. Cone.
Homotopy excision theorem
Let \((A, C)\), \((B, C)\) be Relative CW complex. Let \(X\) be the push-out of \(C \to B\) and \(C \to A\). If \((A, C)\) is m-connected and \((B, C)\) is n-connected, then \[\pi_{i}(A, C) \to \pi_{i}(X, B)\] is an isomorphism for \(i < m + n\) and a surjection for \(i = m + n\).
Homotopy extension property
A map \(i: A \to X\) is said to have the homotopy extension property (HEP) with respect to \(Y\) if for any map \(f:X \to Y\) and any homotopy \(F:A \times I \to Y\), we have following commutative diagram.
Referenced: Cofibration.
Homotopy fiber
Let \(f: X \to Y\), we define its homotopy fiber over \(y \in Y\) to be the fiber of \(P_{f} \to Y\) over \(y\). Then we have
If \(Y\) is path connected, then all homotopy fibers of \(f:X \to Y\) are homotopic equivalent.
Cf. Path connected.
If \(f: X \to Y\) is a fibration, then its homotopy fiber at \(y\) is homootpy equivalent to \(f^{-1}(y)\).
Let \(f:X \to Y\) be a fibration and \(Y\) path connected. Then all fibers of \(f\) are homotpy equivalent.
Therefore, Fibration is similar to Fibre bundle.
Referenced: Exact Puppe sequence, Fibration, Homotopy cofiber.
TODO Homotopy group
Unlike the Fundamental group, the higher homotopy group is abelian.
\(\pi_{n}(X)\) is abelian if \(n \geq 2\).
Referenced: Simplicial homotopy group, Degree, Exact Puppe sequence, Smash product.
Homotopy lifting property
A map \(p: E \to B\) is said to have the homotopy lifting property with respect to \(X\) if for every \(\tilde{f}\) and \(F\) we have \(\tilde{F}\) making the following diagram commutes.
Referenced: Fibration.
Hurewicz theorem
The Hurewicz theorem relates the Homotopy theory and Homology theory. We first fix generator satisfying the compatibility conditions \(i_{n} \in \tilde{H}_{n}(S^{n}) = H_{n}(D^{n}, S^{n - 1}) = \tilde{H}_{n - 1}(S^{n - 1})\). Then we can define Hurewicz map \[\rho: \pi_{n}(X) \to H_{n}(X)\] by sending \([f: S^{n} \to X] \to f_{* }(i_{n})\). Then we have
The Hurewicz map is a group homomorphism.
The Hurewicz theorem states that in certian circumstances the above homomorphism can be isomorphism.
Let \(X\) be a path-connected \((n - 1)\)-connected space. Then the Hurewicz map \[\rho_{n}(\pi_{n}(X)) \to H_{n}(X)\] is the abelianization homomorphism.
Notice that for \(n \geq 2\), the homotopy group \(\pi_{n}(X)\) is already abelian.
The theorem can also be written in relative form.
Let \((X, A)\) be a pair of path-connected spaces and \(A\) non-empty simply connected. If \((X, A)\)is \((n - 1)\)-connected, then \[H_{i}(X,A) = 0 \text{ for } i < n\] and the Hurewicz map \[\pi_{n}(X,A) \to H_{n}(X, A)\] is an isomorphism.
Referenced: Whitehead theorem.
Künneth formula
The algebraic version of Künneth formula is
Let \(C_{\bullet}\) and \(D_{\bullet}\) be chain complex of free abelian groups. Then there is a split exact sequence \[0 \to (H_{\bullet}( C) \otimes H_{\bullet}(D))_{n} \to H_{n}(C_{\bullet} \otimes D_{\bullet}) \to \Tor(H_{\bullet}( C), H_{\bullet}(D))_{n - 1} \to 0\] Here \(\Tor(H_{\bullet}, H_{\bullet}(D))_{k} = \oplus_{p + q = k} \Tor(H_{p}( C), H_{q}(D))\).
Apply the algebraic version to the Singular homology, we have
For any topological spaces \(X, Y\) and \(n \geq 0\), there is a split exact sequence \[0 \to \oplus_{p + q = n} H_{p}(X) \otimes H_{q}(X) \to H_{n}(X \times Y) \to \oplus_{p + q = n - 1} \Tor(H_{p}(X), H_{q}(Y)) \to 0\]
Lefschetz fixed point theorem
The Poincaré duality gives the intersection pairing \[\langle -, - \rangle : H_{i}(X) \times H_{n - i}(X) \to H_{0}(X) \cong \mathbb{Z}\] or equivalently \[\langle -, - \rangle : H^{i}(X) \times H^{n - i}(X) \to H^{n}(X) \cong \mathbb{Z}\]
Cf. Intersection forms.
By consider the intersection of the diagonal \(\Delta\) and the graph of the map \(f\), we get the fixed points of \(f\). We define the Lefschetz number of \(f\) by \[L(f) := \sum_{p}(-1)^{p} \tr(f_{* }: H_{p}(X; \QQ) \to H_{p}(X; \QQ))\] Then we have Lefschetz fixed point theorem
When \(\Gamma_{f}\) and \(\Delta\) intersections transversely, then we have \[\abs{ {\rm Fix}(f)} = L(f)\]
TODO Lifting
The following theorem states when a map can be lifted to its Covering space.
Let \(p: E \to B\) be a covering. Consider a continuous map \(f: X \to B\), where \(X\) is path connected and locally path connected. Let \(e_{0} \in E\), \(x_{0} \in X\) such that \(f(x_{0}) = p(e_{0})\). Then there exists a lift \(F\) of \(f\) with \(F(x_{0}) = e_{0}\) if and only if \[f_{* }(\pi_{1}(X, x_{0})) \subset \pi_{* }(\pi_{1}(E, e_{0}))\]
Cf. Path connected.
Local homology group
Let \(h_{* }(-)\) be a homology theory and \(M\) an \(n\)-dimensional Manifold. Then groups of the form \(h_{k}(M, M \backslash x)\) are called local homology group.
By excision theorem, we have that \(h_{k}(M, M \backslash x)\) is \(h_{k}(D^{n}, D^{n} \backslash x)\). For Singular homology theory, we have \(H_{n}(M, M \backslash x; G) \cong G\) and other homology groups are all \(0\).
For \(K \subset L \subset M\), we have homomorphism \(r_{K}^{L}: h_{k}(M, M \backslash L) \to h_{k}(M, M \backslash K)\).
Referenced: Orientation, Fundamental class.
Local trivial
See Fibre bundle.
Referenced: Covering.
Loop space
Given \((X, x_{0}) \in \cat{CGWH* }\), we define the based loop space \(\Omega_{x_{0}}X\) or simply \(\Omega X\) by \[\Omega X = {\rm Map}_{* }(S^{1}, X)\] And we define the free loop space \[\mathscr{L}X = {\rm Map}(S^{1}, X)\]
Cf. Category CGWH.
Referenced: Arc space.
Mapping cylinder
For \(f: A \to X\), we define the mapping cyclinder \(M_{f}\) by the pushout of \(A \times \{0\} \to A \times I\) and \(A \times \{0\} \to X \times \{0\}\).
For based space, let \(f:(X, x_{0}) \to (Y, y_{0}) \in \cat{CGWH*}\). We define its mapping cylinder by \[M_{*f} = M_{f}/ \{x_{0} \times I\}\]
Mayer-Vietoris sequence
There are Mayer-Vietoris sequence for homology and Cohomology theory. For \((A; A_{0}, A_{1}) \subset (X; X_{0}, X_{1})\) be excisive triads that is \(A = A_{0}^{\circ} \cap A_{1}^{\circ}\) and \(X = X_{0}^{\circ} \cap X_{1}^{\circ}\). Set \(X_{01} = X_{0} \cap X_{1}\) and \(A_{01} = A_{0} \cap A_{1}\). Then we have exact sequence \[\cdots \to h^{n - 1}(X_{01}, A_{01}) \to h^{n}(X, A) \to h^{n}(X_{0}, A_{0}) \oplus h^{n}(X_{1}, A_{1}) \to h^{n}(X_{01}, A_{01}) \to \cdots\]
Referenced: Cohomology, Compactly supported cohomology, Excision theorem.
n-connected
A pair \((X, A)\) is called n-connected if \(\pi_{0}(A) \to \pi_{0}(X)\) is surjective and \[\pi_{k}(X, A; x_{0}) = 0 \; \forall 1 \leq k \leq n, x_{0} \in A\]
Let \(X\) be obtained from \(A\) by attaching \(n\)-cells \((n \geq 1)\), then \((X, A)\) is \((n - 1)\)-connected.
Referenced: Homotopy excision theorem.
Neighborhood deformation retract
Let \(A\) be a subspace of \(X\). \(A\) is called a neighborhood deformation retract if there exists a continuous map \(u: X \to I\) with \(A = u^{-1}(0)\) and a homotopy \(H: X \times I \to X\) such that
\begin{equation} \begin{cases} H(x, 0) = x & \forall x \in X \\ H(a, t) = a & \text{if } (a, t) \in A \times I \\ H(x, 1) \in A & \text{if } u(x) < 1 \end{cases} \end{equation}
If \(A\) is a NDR of \(X\), then \(A\) is a strong Deformation retract of the open subset \(u^{-1}(\rinterval{0}{1})\).
n-equivalence
A map \(f: X \to Y\) is called an n-equivalence if for any \(x_{0} \in X\) we have \(f_{* }: \pi_{r}(X,x_{0}) \to \pi_{r}(Y, f(x_{0}))\) bijective for \(r < n\) and \(f_{* }: \pi_{n}(X, x_{0}) \to \pi_{n}(Y, f(x_{0}))\) is surjective.
Referenced: Weak homotopy equivalence.
Numerable
An open covering is called numerable if it admits a subordinate partition of unity.
Partition of unity is one of the important properties of the covering which deserves its own definition.
A vector bundle (locally trivial bundle) \(\xi: E(\xi) \to B\) is called numerable if there exists a numerable covering on which the vector bundle is trivial.
Cf. Vector bundle
Referenced: Riemannian metric, Classifying Space, Vector bundle.
TODO Path connected
Referenced: Covering, Deck transformation, Homotopy fiber, Lifting, Seifert-Van Kampen theorem, Universal covering.
Path space
Given \(X \in \cat{CGWH}\) and \(x \in X\), we define the free path space \(PX = {\rm Map}(I, X)\) and based path space \(P_{x}X = {\rm Map}((I, 0), (X, x))\).
For \(f: X \to Y\), and \(p_{1}:PY \to Y\), we define the mapping path space \(P_{f}\) by the pull-back \(PY \times_{Y} X\).
Poincaré duality
The Poincaré duality is the following famous theorem.
Given \(X\) an oriented \(n\)-manifold. Then for any \(p\) \[D: H_{c}^{p}(X) \to H_{n - p}(X)\] is an isomorphism. In particular, if \(X\) is compact, then \(H^{p}(X) \cong H_{n - p}(X)\). The isomorphism is given by cap product with the fundamental class of \(X\).
Cf. Orientation, Manifold, Compactly supported cohomology, Singular homology, Fundamental class.
Referenced: Lefschetz fixed point theorem.
Poincaré-Hopf thereom
\(\chi(X) = e(TX) [X] = \sum_{i = 0}^{\dim X}(-1)^{i}b_{i}(X)\), here \(b_{i}(X)\) is the ith betti number.
Cf. Euler class, Vector bundle.
Pontryagin class
The Pontryagin class is defined as \(P_{i}(E) = (-1)^{i}c_{2i}(E \otimes_{\RR} \CC)\), where \(c_{i}\) is the Chern class.
Referenced: Characteristic class for 4-manifold.
TODO Postnikov tower
TODO Properly discontinuous
Referenced: G-principal covering.
Reduced cohomology
The reduced cohomology groups are defined to be \(\tilde{h}^{n}(X) \to \coker(h^{n}(pt) \to h^{n}(X))\) where the map is induced by \(p: X \to pt\).
Cf. Cohomology.
TODO Relative CW complex
Referenced: Cellular approxiamtion theorem, Homotopy excision theorem.
TODO Relative homotopy group
Retraction
Let \(i: A \subset X\) be an inclusion. A continuous map \(r: X \to A\) is called a retraction if \(r \circ i = 1_{A}\). \(r\) is called a deformation retraction if furthermore we have a homotopy \(i \circ r \cong 1_{X} \text{ rel } A\).
Referenced: Deformation retract.
Seifert-Van Kampen theorem
Let \(X = U \cap V\) where \(U, V \subset X\) are open. Then the following diagram
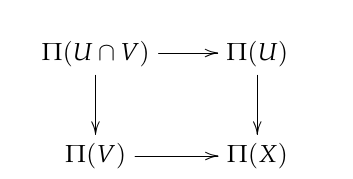
is a pushout in the category \(\cat{Groupoid}\).
Cf. Groupoid, Fundamental groupoid.
Let \(X = U \cap V\) where \(U, V \subset X\) are open and \(U, V, U \cap V\) are path connected. Let \(x_{0} \in U \cap V\). Then the following diagram
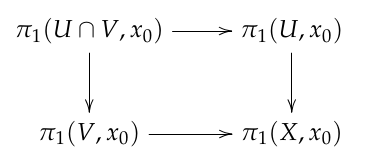 is a pushout in the category \(\cat{Group}\).
is a pushout in the category \(\cat{Group}\).
Cf. Path connected, Fundamental group.
Semi-locally simply connected
A space is semi-locally simply connected if for any \(x_{0} \in X\), there is a neighborhood \(U_{0}\) such that the image of the map \(i_{* }: \pi_{1}(U_{0}, x_{0}) \to \pi_{1}(X, x_{0})\) is trivial.
Cf. Simply connected, Fundamental group.
Referenced: Covering, Universal covering.
TODO Simply connected
Referenced: Semi-locally simply connected, Universal covering.
Smash product
We define the smash product \(\wedge\) by \(X \wedge Y = X \times Y / X \vee Y\).
Cf. Wedge product.
\[S^{1} \wedge S^{n} \cong S^{n + 1}\]
The above example will be used in the computation of Homotopy group of \(S^{n}\).
Referenced: Cone, Suspension.
Standard n-simplex
We denote the standard n-simplex by \(\Delta^{n} = \{(t_{0}, \cdots, t_{n}) \in \RR^{n + 1} \mid \sum_{i = 0}^{n} t_{i} = 1, t_{i} \geq 0\}\).
Referenced: Singular homology.
Stiefel-Whitney class
For \(p: E \to X\) real Vector bundle, we want to find sections linear independent. And we define the Stiefel-Whitney class \(w_{* }(E)\) as the obstruction in \(H^{* }(X; \ZZ/2)\). It is universal for characteristic class in \(\ZZ/2\) coeffecients.
Referenced: Orientation, Characteristic class for 4-manifold, Spin^C structure.
Suspension
We define the suspension of the space \(X\) by \(\Sigma X = X \wedge S^{1}\).
Cf. Smash product.
Referenced: Reduced homology.
TODO Transport functor
Trvialization
See Fibre bundle.
Universal coefficient theorem
The universal coefficient theorem for cohomology gives cohomology from homology.
Let \(G\) be an abelian group and \(X\) be a topological space. Then for any \(n \geq 0\), there exists a split exact sequence \[0 \to \Ext(H_{n - 1}(X), G) \to H^{n}(X; G) \to \Hom(H_{n}(X), G) \to 0\] which induces isomorphisms \[H^{n}(X; G) \cong \Hom(H_{n}(X), G) \oplus \Ext(H_{n -1}(X), G)\]
The universal coefficient theorem for homology gives homology with other coefficients from coefficient \(\ZZ\).
Let \(G\) be an abelian group and \(X\) be a topological space. Then for any \(n \geq 0\), there exists a split exact sequence \[0 \to H_{n}(X) \otimes G \to H_{n}(X; G) \to \Tor(H_{n - 1}(X), G) \to 0\] which induces isomorphisms \[H_{n}(X; G) \cong (H_{n}(X) \otimes G) \oplus \Tor(H_{n - 1}(X), G)\]
The split exact sequence is natural for \(G\) but not for \(X\).
Universal covering
A universal covering is a Covering which is Simply connected.
If \(B\) is path connected, locally path connected, and semi-locally simply connected. Then \(B\) admits a universal covering.
Cf. Path connected, Semi-locally simply connected.
Vector bundle
The Whitney sum of two vector bundle \(\xi: E(\xi) \to B\) and \(\eta: E(\eta) \to B\) is \(d^{* }(\xi \times \eta) = \xi \oplus \eta\), where \(d: B \to B \times B\) is the diagonal map. A bundle \(\eta\) is called an inverse of \(\xi\), if \(\xi \oplus \eta\) is isomorphic to a trivial bundle.
A numerable vector bundle has a Riemann metric.
Cf. Numerable
A bundle has an inverse if and only if it is numerable of finite type.
The real vector bundles and complex vector bundles have monoid structure and can be transformed into Grothendieck ring denoted by \(KO(X)\) and \(K(X) = KU(X)\).
Referenced: Connection, Covariant derivative, Holonomy group, Normal bundle, Tangent bundle, Bott periodicity, Chern class, Complex line bundle over CP^1, Euler class, Fibre bundle, Numerable, Poincaré-Hopf thereom, Stiefel-Whitney class, Elliptic fibration.
Weak Hausdorff
A space \(X\) is weak Hausdorff if for every compact Hausdorff \(K\) and every continuous map \(f:K \to X\), the image \(f(K)\) is closed in \(X\). We denote the full subcategory of weak Hausdorff space by \(\cat{WH}\).
Referenced: Category CGWH.
Weak homotopy equivalence
\(f\) is called weak homotopy equivalence if \(f\) is n-equivalence for any \(n \geq 0\).
Referenced: Weak equivalence, CW approximation, Whitehead theorem.
Wedge product
We define the wedge product \(\vee\) by \(X \vee Y = X \coprod Y / \sim\), where \(\sim\) identifies \(x_{0} \in X\) and \(y_{0} \in Y\).
Referenced: Smash product.
Well-pointed
A based space \((X,x_{0})\) is called well-pointed, if the inclusion of the base point \(x_{0} \in X\) is a Cofibration in the unbased sense.
Whitehead theorem
The Whitehead theorem means that Weak homotopy equivalence is equivalent to homotopy equivalence for CW complexes.
A map between CW complexes is a weak homotopy equivalence if and only if it is a homotopy equivalence.
By Hurewicz theorem, the Whitehead theorem also has an Homology version.
Let \(f: X \to Y\) between simply connected CW complexes. Assume \[f_{* }: H_{n}(X) \to H_{n}(Y)\] is an isomorphism for each \(n\). Then \(f\) is a homotopy equivalence.
TODO Whitehead tower
Algebraic Geometry
There are two tastes of algebraic geometry. The algebraic geometers view it as a specialized geometry, which is closed related to complex geometry (by GAGA), birational geometry (MMP for example), symplectic geometry (Gromov-Witten invariants) etc. Algebraic geometers are mainly interested in case where the base field is \(\CC\). Experts in other field may view algebraic geometry as useful languages, where vast properties are worked out by algebraic geometers. Therefore, Grothendieck’s style of algebraic geometry provides many insights into number theory, representation theory etc. In both case, the characteristic \(p\) case is more interesting. Examples includes Steinberg variety, p-adic Hodge theory.
The following are the themes in Algebraic Geometry Salt Lake 2015 seminar https://sites.google.com/site/2015summerinstitute/home/schedule : analytic methods, birational geometry and classification, commutative algebra and computational algebraic geometry, Hodge theory, singularities and characteristic p methods, derived algebraic geometry, derived categories, geometric representation theory, Gromov-Witten and Donaldson-Thomas theories, mirror symmetry, tropical geometry, algebraic cycles, cohomology theories, p-adic Hodge theory, rational points and Diophantine problems, topology of algebraic varieties
2-Yoneda lemma
The 2-Yoneda lemma is Yoneda lemma for 2-morphisms.
Let \(\mathfrak{X}\) be a prestack over a category \(\mathfrak{S}\) and \(S \in \mathfrak{S}\). The functor \[\cat{Mor}(S, \mathfrak{X}) \to \mathfrak{X}(S), f \to f_{S}(\id_{S})\] is an equivalence of categories, here we view \(S\) as presheaf \(\Hom(-, S)\).
Cf. Prestack.
TODO Affine derived scheme
Affine grassmannian
Let \(G\) affine linear Algebraic group. We define the functor \[{\rm Gr}_{G}( R) = G(R((t)))/G(R[|t|])\] called affine grassmannian. We write \(\mathcal{O} = k[|t|]\) and \(K = k((t))\).
Cf. Loop space, Arc space.
We have Cartan decomposition for \(G(K)\).
\[G(K) = \coprod_{\mu \in X_{*}(T)^{+}} G(\mathcal{O})t^{\mu} G(\mathcal{O})\]
The above theorem gives a stratification of \({\rm Gr}_{G}\)
\[{\rm Gr}_{G} = \coprod_{\mu \in X_{*}(T)^{+}}G(\mathcal{O})t^{\mu} G(\mathcal{O})/ G(\mathcal{O}) = \coprod_{\mu} {\rm Gr}_{\mu}\]
And we have following inclusion properties
For \(G\) reductive, we have \[\overline{{\rm Gr}^{\lambda}} = \cup_{\mu \leq \lambda} {\rm Gr}^{\mu}\]
Affine toric variety
An affine toric variety is an irreducible affine variety \(V\) containing a Torus \(T_{N} \cong (\CC^{* })^{n}\) as a Zariski open subset such that the action of \(T_{N}\) on itself extends to an action on \(V\).
There are several ways of constructing toric varieties. First, consider a finite subset \(\mathscr{A} = \{\chi^{1}, \cdots, \chi^{l}\} \subset \ZZ^{n}\) a lattice equivalent to the character of a torus \((\CC^{* })^{n}\). Then we may consider a map \(\Phi_{\mathscr{A}}(t) = (\chi^{1}(t), \cdots, \chi^{l}(t)), T_{N} \to \CC^{s}\). The Zariski closure of the image is a toric variety denoted by \(Y_{\mathscr{A}}\). The ideal of the affine toric variety is a Toric ideal. Detailed construction can see [CLS2011] p.14-15.
Another construction concerns Affine semigroup. given a affine semigroup \(S\), we have \(\CC[S] = \{\sum_{m \in S} c_{m} \chi^{m} \mid c_{m} \in \CC \text{ and } c_{m} = 0 \text{ for all but finitely many } m\}\), where \(\chi^{m}\) is dependent on the embedding into the lattice \(M\). The multiplication is induced by \(\chi^{m} \cdot \chi^{m'} = \chi^{m + m'}\). We have
Let \(S \subset M\) be an affine semigroup. Then:
- \(\CC[S]\) is an integral domain and finitely generated as \(\CC\)-algebra.
- \(\spec \CC[S]\) is an affine toric variety. If \(S = \NN \mathscr{A}\) for a finite set \(\mathscr{A} \subset M\), then we have \(\spec \CC[S] = Y_{\mathscr{A}}\).
The above construction are equivalent in the sense
Let \(V\) be an affine variety. The followings are equivalent:
- \(V\) is an affine toric variety.
- \(V = Y_{\mathscr{A}}\) for some finite set \(\mathscr{A}\) in a lattice.
- \(V\) is an affine variety defined by a toric ideal.
- \(V = \spec \CC[S]\) for an affine semigroup \(S\).
We consider the relation between sublattice variety and original variety. ([CLS2011] Proposition 1.3.18) For \(N'\) have finite index in \(N\) a sublattice and quotient \(G = N/N'\) and \(\sigma \subset N_{\RR}' = N_{\RR}\) be a Strongly convex Rational Polyhedral cone. Then we have
- There are natural isomorphisms \[G \cong \Hom_{\ZZ}(M'/M, \CC^{* }) = \ker(T_{N'} \to T_{N})\]
- \(G\) acts on \(\CC[\sigma^{\vee} \cap M']\) and \[\CC[\sigma^{\vee} \cap M']^{G} = \CC[\sigma^{\vee} \cap M]\]
- We have bijection \[U_{\sigma, N'}/G \cong U_{\sigma, N}\]
That is the original variety is Geometric quotient of the sublattice varieties.
Referenced: Toric, Face, Pointed, Saturated, Toric variety.
Algebraic group
An algebraic group \(G\) over a field \(k\) is a Group scheme \(G/k\) which is separated and smooth.
Referenced: Representation category, Affine grassmannian, Radical, Unipotent, Unipotent radical, Semisimple, Reductive, Parabolic, Isogeny, Langlands dual pair.
Radical
[milne2017] p.135
Let \(G\) be a connected Algebraic group over \(k\). \(G\) contains a largest connected solvable normal subgroup called the radical, \(R(G)\) of \(G\).
Referenced: Unipotent radical, Semisimple.
Unipotent
[milne2017] p.135
An Algebraic group \(G\) is said to be unipotent if every nonzero representation of \(G\) has a nonzero fixed point. Or equivalently speaking, every finite-dimensional representation \(r: G \to \GL_{V}\) there is a basis such that \(r(G) \subset \U_{n}\).
Unipotent radical
[milne2017] p.135
The unipotent radical of \(G\) is the largest connected normal unipotent sub-Algebraic group of \(G\), denoted by \(R_{u}(G)\).
Cf. Radical.
Referenced: Reductive.
Semisimple
[milne2017] p.135
An Algebraic group is called semisimple if \(R(G_{k^{a}})\) is trivial, where \(k^{a}\) is the algebraic closure of \(k\).
Cf. Radical.
Reductive
[milne2017] p.135
An Algebraic group is called reductive if \(R_{u}(G_{k^{a}})\) is trivial, where \(k^{a}\) is the algebraic closure of \(k\).
Cf. Unipotent radical.
Referenced: Positive root.
Parabolic
A smooth subgroup \(P \subset G\) is parabolic if \(G/P\) complete as algebraic variety.
For \(k\) algebraic closed, a smooth connected algebraic group \(B \subset G\) is minimal among parabolics \(P\) is equivalent to \(B\) solvable parabolic.
Cf. Algebraic group.
Referenced: Borel.
Borel
A algebraic subgroup \(B\) is called Borel if it is Parabolic, smooth, connected and solvable.
Referenced: Positive root.
Algebraic space
An algebraic space is a Sheaf \(X\) on \(\cat{Sch}_{Ét}\) such that there exist a scheme \(U\) and a surjective Étale morphism \(U \to X\) representable by schemes. The morphism \(U \to X\) is called an étale presentation.
Let \(P\) be one of the following property of morphisms of algebraic spaces: open immersion, closed immersion, locally closed immersion, affine, or quasi-affine. Consider the cartesian diagram
such that \(Y' \to Y\) is surjective, flat and locally of finite presentation. Then \(X \to Y\) has \(P\) if and only if \(X' \to Y'\) has \(P\).
For more properties, see Algebraic stack.
Algebraic stack
An algebraic stack is a Stack \(X\) over \(\cat{Sch}_{Ét}\) such that there exist a scheme \(U\) and a surjective, smooth and Representable morphism \(U \to X\). The morphism is called smooth presentation.
A typical example of algebraic stack is the quotient stack, denoted by \([X/G]\), whose object over \(S\) are diagrams
 where \(P \to S\) is a \(G\)-Torsor and \(f: P \to X\) \(G\)-equivaraint. And morphism between objects the following diagram
where \(P \to S\) is a \(G\)-Torsor and \(f: P \to X\) \(G\)-equivaraint. And morphism between objects the following diagram
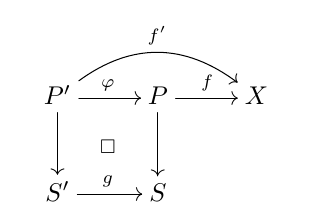
The map \(X \to [X/G]\) is a \(G\)-torsor even when the action is not free.
The flatness, smoothness, surjectivity, locally of finite presentation, locally of finite type are smooth-local and étaleness is étale-local. So all can be defined for Deligne-Mumford stacks but latter can not be defined for algebraic stacks.
We define the topological space of the algebraic stack \(\abs{X}\) as set consisting of field-value moprhisms \(x: \spec K \to X\). Two morphism \(x_{1}: \spec X_{1} \to X\) and \(x_{2}: \spec K_{2} \to X\) if there exists field extension \(K_{3}/K_{1}\) and \(K_{3}/K_{2}\) such that \(x_{1}|_{\spec K_{3}}\) and \(x_{2}|_{\spec K_{3}}\) are isomorphic in \(X(K_{3})\). A subset \(V\) is open if there exists open immersion \(U \ito X\) such that \(V\) is the image of \(\abs{U} \to \abs{X}\).
We say that an algebraic stack is quasi-compact, connected, or irreducible if \(\abs{X}\) is.
A point \(x \in \abs{X}\) is of finite type if there exists a representative \(\spec K \to X\) of finite type.
Let \(R \to U\) be a smooth Groupoid of schemes. Define \([U/R]^{pre}\) to be the prestack whose objects are morphism \(T \to U\) from a scheme \(T\). A morphism \((S \xrightarrow{a} U) \to (T \xrightarrow{b} U)\) is the data of a morphism of schemes \(f: S \to T\) and an element \(r \in R(S)\) such that \(s( r) = a\) and \(t( r) = f \circ b\). Define \([U/R]\) to be the stackification of \([U/R]^{pre}\).
Let \(R \to U\) be an étale (resp. smooth) groupoid of schemes. Then \([U/R]\) is a Deligne-Mumford stack (resp. algebraic stack) and \(U \to [U/R]\) is an étale (resp. smooth) presentation.
The diagonal of an algebraic space is representable by schemes.
The diagonal of an algebraic stack is representable.
Any morphism from a scheme to an algebraic space is representable by schemes.
Any morphism from a scheme to an algebraic stack is representable.
If \(R \to U\) be an étale equivalence relation of schemes, then \(U/R\) is an algebraic space and \(U \to U/R\) is an étale morphism.
- A morphism of algebraic stack \(X \to Y\) is quasi-separated if \(X \to X \times_{Y} X\) is quasi-compact.
- A representable morphism \(X \to Y\) of algebraic stacks is separated if the morphism \(X \to X \times_{Y} X\) is representable by schemes and proper.
- An algebraic stack \(X\) is quasi-separated if it is quasi-separated over \(\spec \ZZ\).
- An algebraic stack \(X\) is noetherian if it is locally noetherian, quasi-compact and quasi-separated.
Let \(X\) be a noetherian algebraic space and \(x \in \abs{X}\). We define the dimension of \(X\) at \(x\) to be \[\dim_{x} X = \dim_{u} U \in \mathbb{Z}_{\geq 0} \cup \infty\] where \(U \to X\) is any étale presentation and \(u \in U\) is an preimage.
Let \(X\) be an algebraic stack with smooth presentation \(U \to X\) and corresponding smooth groupoid \(s, t: R \to U\), and let \(u \in U\) be a preimage of \(x \in \abs{X}\). We define the dimension of \(X\) at \(x\) to be \[\dim_{x} X = \dim_{u} U - \dim_{e(u)} R_{u} \in \ZZ \cup \infty\] where \(R_{u}\) is the fiber of \(s: R \to U\) over \(u\) and \(e: U \to R\) denotes the identity morphism in the groupoid.
If \(X\) is a noetherian algebraic space or stack, we define the dimension of \(X\) to be \[\dim X = \sup \dim_{x} X \in \ZZ \cup \infty\]
If \(X\) is an algebraic stack and \(x: \spec k \to X\), we define the Zariski tangent space or simply the tangent space of \(X\) at \(x\) as the set \[T_{X,x} = \{f:\spec k[\epsilon] \to X, \alpha: x \cong f|_{spec k}\}/ \sim\] where two pairs are equivalent if there is an isomorphism between them.
If \(X\) is an algebraic stack with affine diagonal and \(x \in X(k)\), then \(T_{X,x}\) is naturally a \(k\)-vector space.
Arc space
We define the arc space to be functor \(Y[|t|]\) such that \(Y[|t|]( R) = Y(R[|t|])\).
Cf. Loop space.
Arc spaces and \(Y[k[t]/t^{n}]\) are schemes. Moreover, if \(Y\) is affine then they are also affine.
Referenced: Affine grassmannian, Loop space.
Auslander-Buchsbaum formula
Let \(A\) be a regular ring, then we have \[\dimh(M) + \depth(M) = \dim (A)\] Cf. Homological dimension, Depth.
Calabi-Yau variety
Referenced: Donaldson-Thomas theory, Kähler manifold with holomorphic symplectic structure.
Castelnuovo theorem
The Castelnuovo theorem classified the mimimal surfaces.
Two birational minimal models are isomorphic unless they are both birational to a ruled surface \(C \times \CC P^{1}\).
Categorical quotient
Given an action \(\sigma\) of \(G/S\) on \(X/S\), a pair \((Y, \phi: X \to Y)\) is called a categorical quotient if we have diagram
 commutes and universal property that for any \((Z, \psi)\) satisfying the above diagram, there exists a unique morphism \(\chi: Y \to Z\) such that \(\psi = \chi \circ \phi\).
commutes and universal property that for any \((Z, \psi)\) satisfying the above diagram, there exists a unique morphism \(\chi: Y \to Z\) such that \(\psi = \chi \circ \phi\).
A categorical quotient is called universal if it is stable under base change, and is called uniform if it is stable under flat base change.
Referenced: Geometric quotient.
Category of modules
Let \(T\) be a Topos and let \(\Lambda\) be a ring in \(T\). Denote by \(\cat{Mod}_{\Lambda}\) the category of \(\Lambda\)-modules in \(T\).
The category \(\cat{Mod}_{\Lambda}\) is an abelian category with enough injectives.
Then we have functor \[\Gamma(T, -): \cat{Mod}_{\Lambda} \to \cat{Ab}\] obtained by \[F \to \Hom_{\cat{Mod}_{\Lambda}}(\Lambda, F)\] This is a left exact functor, and we denote the resulting right derived functor by \(H^{i}(T, -)\), called cohomology functor.
Cf. Cohomology.
Character (of a torus)
A character of a Torus is a group homomorphism \(\chi: T \to \CC^{* }\).
TODO Coarse moduli space
TODO Cohen strcuture theorem
Let \(X\) be a locally Noetherian scheme over a field \(k\), having dimension \(n\) at a smooth point \(x\). Then \(\hat{\OO}_{X,x} \cong k(x)[ [x_{1}, \cdots, x_{n}]]\).
Deformation functor
A Predeformation functor is called a deformation functor if it satisfies (1-2) in Schlessinger’s theorem.
Deligne-Mumford stack
A Deligne-Mumford stack is a stack \(X\) over \(\cat{Sch}_{Ét}\) such that there exist a scheme \(U\) and a surjective, Étale and Representable morphism \(U \to X\). The morphism is also called étale presentation.
For properties, see Algebraic stack.
Cf. Algebraic space.
Depth
The maximal length of an \(M\)-Regular sequence is called the depth of \(M\).
Referenced: Auslander-Buchsbaum formula.
TODO Derived stack
Examples: Betti stack, de Rham stack
Determinant bundle
If \(E\) is locally free of rank \(s\), then the determinant bundle \(\det(E)\) is by definition the line bundle \(\wedge^{s}(E)\). Let \(E\) be arbitrary coherent sheaf. Then we consider a finite locally free resolution \[0 \to E_{n} \to \cdots \to E_{0} \to E \to 0\] And define \(\det(E) = \otimes \det(E_{i})^{(-1)^{i}}\).
If \(\dim(E) \leq \dim(X) - 2\), then we have that \(\det(E) \cong \OO_{X}\).
Different characters may give same toric variety
Exercise 1.1.6 in [CLS2011]. We consider two map \[\Phi_{1}(s,t) = (s^{2}, st, st^{3}), \quad \Phi_{2}(s,t) = (s^{3}, st, t^{3})\] We can show that \(\Phi_{1}\) and \(\Phi_{2}\) gives same affine toric variety. However \(\Phi_{2}\) is surjective and \(\Phi_{1}\) is not.
Donaldson-Thomas theory
Cf. Enumerative geometry.
We consider the case when \({\rm dim}_{\CC}(X) = 3\). We fix a class \(\beta \in H_{2}(X, \ZZ)\) and fix an integer \(\chi \in \ZZ\). The Donaldson-Thomas theory describes the intersection theory on Hilbert scheme of \(X\). Due to existence of nonvanishing higher \({\rm Ext}\) group, the deformation-obstruction theory and Virtual fundamental class of virtual fundamental class is not well-defined. To remedy the issue, we consider \(I_{\chi}(X, \beta)\) parametrizing pairs \((E, \phi)\) such that
- \(E\) is a torsion free sheaf on \(X\) of rank \(1\).
- \(E\) is equipped with a trivialization \(\phi: \det E \cong \mathbb{O}_{X}\).
- The numerical invariants of \(E\) is given by \(c_{2}(E) = - \beta\), \(\xi(E) = \xi(\mathbb{O}_{X}) - \chi\).
The natural map \[{\rm Hilb}_{\chi}(X, \beta) \to I_{\chi}(X, \beta)\] \[Z \to J_{Z}\] is an isomorphism on the level of closed points.
The expected dimension is given by \(\dim(\Ext_{0}^{1}(E, E)) - \dim(\Ext_{0}^{2}(E,E))\), where \(\Ext_{0}\) denote the trace free subspace. So we have that \(\virdim I_{\chi}(X, \beta) = \chi(E, E) - \chi(\OO) = -K_{X} \cdot \beta\). In Gromov-Witten theory, we also have the fundamental class of dimension equal to \(-K_{X} \cdot \beta\). So if \(X\) is Calabi-Yau variety, we have \(\virdim I_{\chi}(X, \beta) = 0\).
We don’t have evaluation map in Donaldson-Thomas theory, so we consider \[\tilde{J} \to \hilb(X) \times X\] for the purpose of integration. Given \(\alpha \in H^{*}(X)\), we can define an operator \[\sigma_{0}(\alpha): \pi_{\hilb *}(- \ch_{2}(\tilde{J}) \cup \pi_{X}^{*}(\alpha) \cap \pi_{\hilb}^{*}(-)), H_{*}(\hilb(X)) \to H_{*}(\hilb(X))\] Then the Donaldson-Thomas invariants are defined by
\begin{align}\langle \alpha_{1}, \cdots, \alpha_{n} \rangle^{DT}_{\beta, m} &= \deg \prod_{k} \sigma_{0}(\alpha_{k})[I_{\chi}(X, \beta)]^{vir} \\ &= \int_{ [I_{\chi}(X, \beta)]^{vir}} \prod_{k} \sigma_{0}(\alpha_{k}) \\ &= \int_{ [I_{\chi}(X, \beta)]^{vir}} \prod_{k} \pi_{\hilb *}(- \ch_{2}(\tilde{J}) \cup \pi_{X}^{*}(\alpha_{k}) \cap \pi^{*} \beta)\end{align}
Here note \(-\ch_{2}(I_{Z}) = \beta\) is represented by cycle class \(Z \subset X\).
There may be some mistakes in definition, because I suppose that the second line is not well-defined and the \(\beta\) in the last line is unnatural. However, I don’t know the correct algebraic definition of Donaldson-Thomas theory yet. So I still follow the definition in GW/DT Theory Lecture 11.
Dual sheaf
Let \(E\) be a coherent sheaf of codimension \(c\). The dual sheaf is defined as \(E^{D} = \sext^{c}_{X} (E, \omega_{X})\).
Referenced: Reflexive.
Enumerative geometry
There are several aspects of enumerative geometry, beyond the numbers.
- counting curves and sheaves (Gromov-Witten theory, Donaldson-Thomas and related theories)
- gauge theory enumerative geometry (3d gauge theories and Coulomb branches, mirror symmetry, 4d gauge theories, and Vafa-Witten invariants, etc)
- applications of enumerative geometry to categorification and low-dimensional topology
- Hall algebras and their refined versions (cohomological, K-theoretic, derived categories)
- Enumerative geometry of Nakajima quiver variety and the representation of quantum groups (symplectic resolution, etc)
Referenced: Donaldson-Thomas theory, Gromov-Witten theory.
Étale site
See Site.
:ID: e75a7770-d111-4f5e-9fb0-72a34c894b6e
See Site.
TODO Exact sequence about extensions
See [sernesi2006] Proposition 1.1.5, Proposition 1.1.7, and Corollary 1.1.8.
The proof in my mind is straightforward but a little tricky when manipulate the objects, since sometimes we need to consider the \(R\)-module structure and sometimes as \(A\)-algebra.
Referenced: Extension.
Ex_A(R,I)
See [sernesi2006] p.12.
We now consider all isomorphism class of \(A\)-Extensions of \(R\) by \(I\), called \(\ex_{A}(R,I)\). We want to show that \(\ex_{A}(R, I)\) is an \(R\)-module. We first construct the pullback and pushout for extensions. We define the pullback, denoted by \(f^{* }(R', \phi)\) by following diagram:
 And define the pushout by the other, denoted by \(\lambda_{*}(R', \phi)\):
And define the pushout by the other, denoted by \(\lambda_{*}(R', \phi)\):
 Where
\[R' \coprod_{I} J = \frac{R' \tilde{\oplus} J}{\{(- \alpha(i), \lambda(i)), i \in I\}}\]
Where
\[R' \coprod_{I} J = \frac{R' \tilde{\oplus} J}{\{(- \alpha(i), \lambda(i)), i \in I\}}\]
Now we are ready to define the \(R\)-module structure on \(\ex_{A}(R, I)\). If \(r \in R\), we define \(r[R', \phi] = [r_{* }(R', \phi)]\) where \(r: I \to I\) is multiplication by \(r\). And for some, we consider \(R' \times_{R} R''\) as the extension of \(R\) by \(I \oplus I\). And consider the pushout of the function \(\delta: I \oplus I \to I\), such that \(\delta(i \oplus j) = i + j\).
By above construction, \(\ex_{A}(R, -)\) is a covariant functor from \(R\)-modules to \(R\)-modules.
Referenced: Extension, First cotangent module.
Extension
See [sernesi2006] p.9.
Let \(A \to R\) be a ring homomorphism. An \(A\)-extension of \(R\) by \(I\) is an exact sequence \[(R', \phi) : 0 \to I \to R' \stackrel{\phi}{\to} R \to 0\] where \(R'\) is an \(A\)-algebra and \(\phi\) is a homomorphism of \(A\)-algebras whose kernel \(I\) is an ideal of \(R'\) satisfying \(I^{2} = (0)\) which makes \(I\) a \(R\)-module.
Two extensions are isomorphic if the following diagram commutes:
 Here \(\chi\) is an isomorphism of \(A\)-algebras. Similarly, we can define the homomorphism of extensions.
Here \(\chi\) is an isomorphism of \(A\)-algebras. Similarly, we can define the homomorphism of extensions.
Here \(R'\) has to be an \(A\)-algebras, and therefore rings. And \(\chi\) has to be algebra homomorphism. Instead \(I\) only has \(R\)-module structure and may not be rings in general.
The \(A\)-extension \((R', \phi)\) is called trivial if it has a section, that is we have ring homomorphism \(\psi :R \to R'\) such that \(\phi \circ \phi = 1_{R}\). In that case, we say \((R', \phi)\) splits and \(\psi\) is called a splitting.
Examples: dual number, small extension. See [sernesi2006] p.11.
The extension of algebras can be extended to extension of schemes. An extension of \(X/S\) is a closed immersion \(X \subset X'\), where \(X'\) is an \(S\)-scheme, defined by a sheaf of ideals \(\mathscr{I} \subset \mathscr{O}_{X'}\) such that \(\mathscr{I}^{2} = 0\). The isomorphism, homomorphism, triviality, and \(\ex(X/S, \mathscr{I})\) is similar to the algebra case. For details, see [sernesi2006] p.15. (Cf. Ex_A(R,I) and Exact sequence about extensions)
In particular, we have following theorem relating the deformation to the \(\Ext\) groups.
Let \(X \to S\) be a morphism of finite type of schemes and \(\mathscr{I}\) a coherent locally free sheaf on \(X\). Suppose that \(X\) reduced and \(S\)-smooth on a dense open subset. Then there is a cononical equivalence \[\ex(X/S, \mathscr{I}) = \Ext^{1}_{\mathscr{O}_{X}}(\Omega_{X/S}^{1}, \mathscr{I})\] which maps the extension \[\mathscr{E}: 0 \to \mathscr{I} \to \OO_{X'} \to \OO_{X} \to 0\] to \[c_{\mathscr{E}}: 0 \to \mathscr{I} \to (\Omega^{1}_{X'/S})|_{X} \to \Omega^{1}_{X/S} \to 0\]
Referenced: Ex_A(R,I), Versal extension.
Fiber category
Given a Prestack \(\mathfrak{X}\), the fiber category \(\mathfrak{X}(S)\) is the category of objects over \(S\) whose morphisms are over \(\id_{S}\).
TODO Fine moduli space
First cotangent module
See [sernesi2006] p.14.
The \(R\)-module \(\ex_{A}(R,R)\) is called the first cotangent module of \(R\) over \(A\), and is denoted by \(T_{R/A}^{1}\). We omit \(A\) if \(A = k\). The first cotagent sheaf is obtained by gluing the first cotangent modules.
Cf. Ex_A(R,I).
Flat
A \(R\)-module \(M\) is called flat if tensoring with \(M\) is an exact functor.
Fppf site
See Site.
Framed moduli space
See [nakajima1999] p.17.
We define \(\mathscr{M}(r,n)\), the framed moduli space of torsion free Sheaves on \(\PP^{2}\) with rank (r) and \(c_{2} = n\). That is the isomorphism class of pairs \((E, \Phi)\) on \(\PP^{2}\) with \(\rk(E) = n\) \(c_{2}(E) = n\) which is locally free in a neighborhood of \(l_{\infty}\) such that \(\Phi: E|_{l_{\infty}} \ito \mathscr{O}_{l_{\infty}}^{\oplus r}\). The latter isomorphism is called framing at infinity.
We have following simple characterization of framed moduli space.
There exists a bijection between \(\mathscr{M}(r,n)\) and pairs \((B_{1}, B_{2}, i, j)\) such that \([B_{1}, B_{2}] + ij = 0\), and stability condition there exists no proper subspace \(S \subsetneq \CC^{n}\) such that \(B_{\alpha}(S) \subset S\) and \(\im i \subset S\) modulo the action of \(\GL_{n}(\CC)\). Here \(B_{1}, B_{2} \in \End(\CC^{n})\), \(i \in \Hom(\CC^{r}, \CC^{n})\) and \(j \in \Hom(\CC^{n}, \CC^{r})\) with the action \[g \cdot (B_{1}, B_{2}, i, j) = (gB_{1}g^{-1}, gB_{2}g^{-1}, gi, jg^{-1})\]
Cf. Hilb(A^2,n).
There is a interesting lemma with basic techniques in linear algebra.
When \(r = 1\) and \(B_{1}, B_{2}, i, j\) same as above theorem, for \(ij + [B_{1}, B_{2}] = 0\), we have that \(ji = 0\).
See [nakajima1999] p.26. We have \(S^{n}(\CC^{2}) \cong \{(B_{1}, B_{2}, i, j) \mid [B_{1}, B_{2}] + i j = 0\} // \GL_{n}(\CC)\), where \(//\) denote the algebro-geometric quotient.
Cf. Geometric quotient.
Generalized Serre’s condition
We define the generalized Serre’s condition \(S_{k,c}\) as \[\depth(E_{x} \geq \min \{k, \dim(\OO_{X,x}) - c\}) \text{ for all } x \in \supp(E)\]
Geometric quotient
Given an action \(\sigma\) of \(G/S\) on \(X/S\), a pair \((Y, \phi: X \to Y)\) is called a categorical quotient if we have
diagram
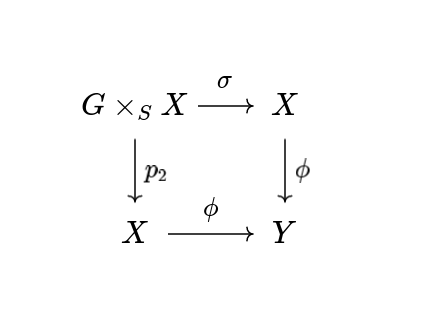 commutes.
commutes.\(\phi\) is surjective and image of \(\Psi = \phi_{\id_{X}}\) is \(X \times_{S} X\) (equivalently the geometric fiber of \(\phi\) are precisely the orbits of the geometric points of \(X\) for geometric points over an algebraic closed field of sufficiently high transcendence degree).
\(\phi\) is submersion that is \(U \subset Y\) is open if and only if \(\phi^{-1}(U)\) is open in \(X\).
The fundamental sheaf \(\OO_{Y}\) is the subsheaf of \(\phi_{* }(\OO_{X})\) consisting of invariant functions, i.e., if \(f \in \Gamma(U, \phi_{* }(\OO_{X})) = \Gamma(\phi^{-1}(U), \OO_{X})\), then \(f \in \Gamma(U, \OO_{Y})\) if and only if
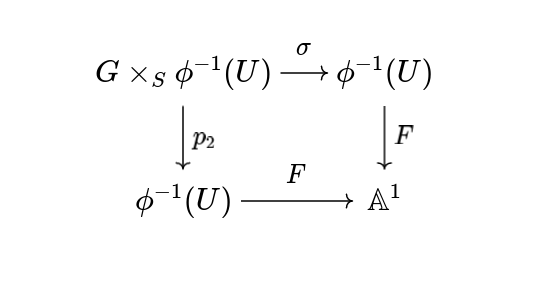
commutes, where \(F\) is the function induced by \(f\).
A geometric quotient is called universal if it is stable under base change, and is called uniform if it is stable under flat base change.
The geometric quotient is related to Categorical quotient by the following proposition.
Given an action \(\sigma\) of \(G/S\) over \(X/S\), and \((Y, \phi)\) is a geometric quotient. Then \((Y, \phi)\) is also a categorical quotient and hence unique. If \((Y, \phi)\) is the universal geometric quotient, then it is also a universal categorical quotient.
Referenced: Affine toric variety, Framed moduli space.
Gromov-Witten theory
Cf. Enumerative geometry.
We have natural maps for Moduli space of Stable Maps
And we have Gromov-Witten class \[I_{g,n,\beta}(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}) = \pi_{2!} (\pi_{1}^{* }(\alpha_{1} \otimes \cdots \otimes \alpha_{n}))\] Also we have Gromov-Witten invariant \[\langle I_{g,n,\beta}(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}) \rangle = \int_{\overline{M}_{g,n}} I_{g,n,\beta}(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}) \]
The Gromov-Witten invariants has natural enumerative geometric interpretation. \(\langle I_{g,n,\beta}(\alpha_{1}, \cdots, \alpha_{n}) \rangle\) equals the number of stable curves in \((C, p_{1}, \cdots, p_{n}) \in \overline{M}_{g,n}\) for which we can find \(f\) such that \(f(p_{i}) \in Z_{i} = \alpha_{i}^{\vee}\) and \(f_{*}( C) = \beta\).
By above interpretation we have natural axioms about Gromov-Witten invariants.
Referenced: Donaldson-Thomas theory, Linear axiom, Effectivity axiom, Degree axiom, Equivariant axiom, Fundamental class axiom, Divisor axiom, Point mapping axiom, Splitting axiom, Reduction axiom, Deformation axiom, Kontsevich recursion formula.
Linear axiom
Cf. Gromov-Witten theory. \(I_{g,n,\beta}\) is linear in each variable.
Effectivity axiom
Cf. Gromov-Witten theory. For \(X\) projective, \(I_{g,n,\beta} = 0\) if \(\beta\) is not an effective curve class.
Degree axiom
Cf. Gromov-Witten theory. For \(\alpha_{1}, \cdots, \alpha_{n} \in H^{* }(X, \mathbb{Q})^{\otimes n}\), \(I_{g,n, \beta}(\alpha_{1}, \cdots, \alpha_{n}) \in H^{* }(\bar{M}_{g,n}, \mathbb{Q})\) has degree \(2 (g - 1) {\rm dim} X + 2 \int_{\beta} \omega_{X} + \sum_{i} {\rm deg} \alpha_{i}\)
Equivariant axiom
Cf. Gromov-Witten theory. The map \(I_{g,n, \beta}\) is \(S_{n}\) equivariant where \(S^{n}\) acts on \(H^{* }(X, \mathbb{Q})^{\otimes n}\) naturally and acts on \(H^{ * }(\overline{M}_{g,n}), \mathbb{Q}\) by permuting \(p_{i}\)’s of the pointed curves.
Fundamental class axiom
Cf. Gromov-Witten theory. If \(n + 2g \geq 4\) then there exists a natural forgetting map \[\pi_{n}: \bar{M}_{g,n} \to \bar{M}_{g,n - 1}\] if \([X] \in H^{0}(X, \mathbb{Q})\) fundamental cycle, then we have that \[I_{g,n, \beta}(\alpha_{1}, \cdots, \alpha_{n - 1}, [X]) = \pi_{n}^{* }I_{g,n-1, \beta}(\alpha_{1}, \cdots, \alpha_{n - 1})\]
Divisor axiom
Cf. Gromov-Witten theory. If \(n + 2g \geq 4\), then \(\pi_{n}: \bar{M}_{g,n} \to \bar{M}_{g,n - 1}\) as above, if \(\alpha_{n} \in H^{2}(X, \mathbb{Q})\) then we have \[\pi_{n * } I_{g,n, \beta}(\alpha_{1}, \cdots, \alpha_{n}) = (\int_{\beta} \alpha_{n}) \times I_{g,n -1, \beta}(\alpha_{1}, \cdots, \alpha_{n-1})\]
Point mapping axiom
Cf. Gromov-Witten theory. When \(\beta = 0\), if \(\alpha_{i}\) are homogeneous cohomology classes, then \[I_{0,n,0}(\alpha_{1}, \cdots, \alpha_{n}) = \int_{X}(\alpha_{1} \cup \cdots \cup \alpha_{n})[\bar{M}_{g,n}]\] if \(\sum_{i} {\rm deg} \alpha_{i} = 2 {\rm dim} X\) and is zero otherwise.
Splitting axiom
Cf. Gromov-Witten theory. By gluing \(2\) points, we have natural map \[C: \bar{M}_{g_{1}, n_{1} + 1} \times \bar{M}_{g_{2}, n_{2} +1} \to \bar{M}_{g,n}\] where \(g = g_{1} + g_{2}\) and \(n = n_{1} + n_{2}\). Then we have \[\phi^{* }I_{g,n, \beta} (\alpha_{1}, \cdots, \alpha_{n}) = \sum_{\beta = \beta_{1} + \beta_{2}} \sum_{i,j} g^{ij}I_{g_{1}, n_{1} + 1, \beta}(\alpha_{1}, \cdots, \alpha_{n_{1}}, T_{i}) \otimes I_{g_{2}, n_{2} +1, \beta_{2}}(T_{j}, \alpha_{n_{1}+ 1}, \cdots, \alpha_{n})\] where \(\phi\) is the diagonal map and \(g^{ij}\) is the inverse matrix of \(g_{ij} = \int_{X} T_{i} \cup T_{j}\).
Reduction axiom
Cf. Gromov-Witten theory. Gluing two point together, we have natural map \(\psi: \bar{M}_{g - 1, n + 2} \to \bar{M}_{g, n}\). Then we have \[\psi^{* } I_{g,n, \beta}(\alpha_{1}, \cdots, \alpha_{n}) = \sum_{i,j}g^{ij}I_{g - 1, n +2, \beta}(\alpha_{1}, \cdots, \alpha_{n}, T_{i}, T_{j})\]
Deformation axiom
Cf. Gromov-Witten theory. Let \(X \to T\) be a smooth proper amp with connected base \(T\). And set \(X_{t}\) is the fiber. Then for each \(t \in T\) and \(\beta_{t} \in H_{2}(X_{t}, \mathbb{Z})\), we obtain a map \(I_{g,n, \beta_{t}}: H^{* }(X_{t}, \mathbb{Q}) \to H^{* }(M_{g,n}, \mathbb{Q})\). Then if \(\beta_{t}\) is locally constant section of \(H_{2}(X_{t}, \mathbb{Q})\) and \(\alpha_{1}, \cdots, \alpha_{n}\) are locally constant, then we have \(I_{g,n, \beta_{t}}(\alpha_{1}, \cdots, \alpha_{n})\) is constant.
Kontsevich recursion formula
Cf. Gromov-Witten theory. For \(X = \mathbb{P}^{2}\), we denote that \(N_{d} = \langle I_{0, 3d - 1, d}([pt], \cdots, [pt]) \rangle \) where \([pt]\) occur \(3d - 1\) times for \(d \geq 1\). Then we have following Kontsevich recursion formula \[N_{d} = \sum_{d = d_{1} + d_{2}, d_{1}, d_{2} > 0} N_{d_{1}}N_{d_{2}} (d_{1}^{2}d_{2}^{2} \binom{3d - 4}{3d_{1} - 2} - d_{1}^{3}d_{2} \binom{3d - 4}{3d_{1} - 1})\]
Grothendieck topology
Let \(C\) be a category. A Grothendieck topology on \(C\) consists of a set \(\cat{Cov}(X)\) of collections of moprhisms \(\{X_{i} \to X\}_{i \in I}\) for every object \(X \in C\) such that the following hold:
- If \(V \to X\) is an isomorphism, then \(\{V \to X\} \in \cat{Cov}(X)\).
- If \(\{X_{i} \to X\}_{i \in I} \in \cat{Cov}(X)\) and \(Y \to X\) is any arrow in \(C\), then the fiber products \(X_{i} \times_{X} Y\) exist in \(C\) and the collection \[\{X_{i} \times_{X} Y \to Y\}_{i \in I}\] is in \(\cat{Cov}(Y)\).
- If \(\{X_{i} \to X\}_{i \in I} \in \cat{Cov}(X)\) and if for every \(i \in I\) we are given \(\{V_{ij} \to X_{i}\}_{j \in J_{i}} \in \cat{Cov}(X)\), then the collection of compositions \[\{V_{ij} \to X_{i} \to X\}_{i \in I, j \in J_{i}}\] is in \(\cat{Cov}(X)\).
The Grothendieck topology is also called a pre-topology.
Referenced: Site.
Group scheme
A group scheme \(G/S\) is a morphism \(\pi: G \to S\) of schemes with \(S\)-morphism multiplication \(\mu: G \times_{S} G \to G\), inverse \(\beta: G \to G\) identity \(e: S \to G\) satisfying associativity, law of inverse and law of identity.
A group scheme \(G\) action on a scheme \(X/S\) is given by a morphism \(\sigma: G \times_{S} X \to X\) with associativity property and identity.
Let \(f: T \to X\) be a \(T\)-valued point. We have morphism \(\phi_{f} = \sigma \circ (1_{G} \times f): G \times_{S} T \to X \times_{S} T\). The image of \(\phi_{f}\) is called the orbit of \(f\) and denoted by \(O(f)\). The fibre product \(S(f)\) is called stabilizer of \(f\). The orbit and stabilizer is the algebraic version of orbit and stabilizer in action on topological spaces.
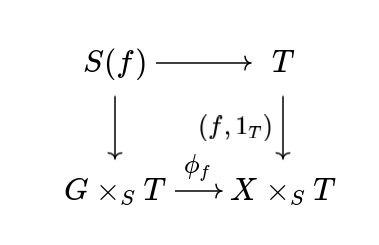
Referenced: Criterion for category being representation category, Reconstruction theorem, Algebraic group.
Groupoid of schemes
See Introduction to Stacks and Moduli p.79.
Hilb(A^2,n)
See [nakajima1999], Theorem 1.9.
We have a specific characterization of \(\hilb(A^{2}, n)\). Let \[\tilde{H} = \{(B_{1}, B_{2}, i) \mid [B_{1}, B_{2}] = 0 \text{ and stable}\}\] The triple \((B_{1}, B_{2}, i)\) is called stable if there exists no proper subspace \(S \subsetneq k^{n}\) such that \(B_{\alpha}(S) \subset S\), \(\alpha = 0,1\) and \(\im i \subset S\). \(B_{\alpha} \in \End(k^{n}) \) and \(i \in \Hom(k, k^{n})\). We have a natural \(\GL_{n}\) action on \(\tilde{H}\) defined by \((B_{1}, B_{2}, i) \to (gB_{1}g^{-1}, gB_{2}g^{-1}, gi)\). And by quotient, we define \(H = \tilde{H}/ \GL_{n}\). And we have that \(H \cong \hilb(\mathbb{A}^{2},n)\).
Cf. Hilbert scheme.
The manifold \(\hilb(\mathbb{A}^{2}, n)\) admits a hyper-Kähler metric.
Referenced: Framed moduli space.
Hilbert-Chow morphism
For Hilbert scheme of points, we have a well define map \[\pi:X^{ [n]}_{red} \to S^{n}X\] by \(\pi(Z) = \sum_{x \in X}l(Z_{x})[x]\), here \(l\) denote the length.
Referenced: Smoothness of Hilbert scheme.
Hilbert scheme
We fix a class \(\beta \in H_{2}(X, \ZZ)\) and fix an integer \(\chi \in \ZZ\).
The Hilbert scheme \({\rm Hilb}_{\chi}(X, \beta)\) parametrizes \(1\) dimensional subscheme \(Z \subset X\) whose irreducible components are at most \(1\)-dimension with numerical invariants \(\beta = [Z] \in H_{2}(X, \ZZ)\) and \(\chi(\mathscr{O}_{Z}) = \chi\).
In [nakajima1999], there is another notation of Hilbert schemes, where in \(\hilb(X, p)\), the \(p\) denote the Hilbert polynomial. And we write \(X^{ [n]}\) for \(\hilb(X, n)\) for Hilbert scheme of points.
Referenced: Donaldson-Thomas theory, Hilb(A^2,n), Hilbert-Chow morphism, Simple resolution, Smoothness of Hilbert scheme, Symplectic structure of Hilbert scheme.
Homological dimension
Let \(M\) be a module of a local ring \(A\). The homological dimension denoted by \(\dimh(M)\) is defined as the minimal length of a projective resolution of \(M\). It is also the length of free resolution of \(M\).
Referenced: Auslander-Buchsbaum formula.
Hull
Let \(F\) be a Predeformation functor and \(\hat{F}\) its completeion. We say a pair \((R, \eta)\) with \(R\) a Noetherian Complete Local ring, and \(\eta \in \hat{F}( R)\), is a hull for \(F\) if the induced map \(\bar{h}_{R} \to F\) is smooth, and induces a bijection \(T_{\bar{h}_{R}} \ito T_{F}\) on tangent spaces.
Referenced: Schlessinger’s theorem.
TODO Hyper-Kähler quotient
Ind-scheme
An ind-scheme is object in \(\cat{Fun}(\cat{k-algebra}, \cat{Set})\) which can be written as \[X = \varinjlim_{I} X_{i}\] such that \(I\) is a direct diagram, \(X_{i}\) is a scheme, all maps \(X_{i} \to X_{j}\) are closed embedding. We call ind-affine, ind-projective, ind-finite type if all \(X_{i}\) are affine, projective, finite type.
Referenced: Loop space.
Inertia stack
The inertia stack of an Algebraic stack \(X\) is the fiber product
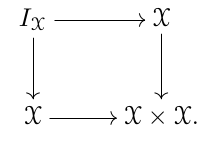
Isogeny
An isogeny is a surjective homomorphism between smooth connected Algebraic groups \(\phi: G \to G'\) with finite kernel \(K\). The degree of \(\phi\) is given by \(\abs{K}\).
See also Isogeny.
Referenced: Degree.
TODO Jacobian criterion
TODO K3 surfaces
Referenced: Intersection forms.
Kähler manifold with holomorphic symplectic structure
See [nakajima1999], Proposition 1.19.
The following proposition may be useful.
Let \(X\) be a compact Kähler manifold which admits a holomorphic symplectic structure. Then \(X\) has a hyper-Kähler structure.
Cf. Calabi-Yau variety, Holonomy group.
Lattice
A lattice is a free abelian group of finite rank.
Referenced: Lattice ideal, Rational, Affine semigroup.
Lattice ideal
Let \(L \subset \ZZ^{s}\) be a sublattice. Then we call the ideal \(I_{L} = \langle x^{\alpha} - x^{\beta} \mid \alpha, \beta \in \NN^{s} \text{ and } \alpha - \beta \in L \rangle\) lattice ideal.
Cf. Lattice.
Referenced: Toric ideal.
TODO Linearly reductive
Loop space
We define the loop space to be functor \(Y((t))( R) = Y(R((t)))\).
Cf. Arc space.
The loop space is ind-scheme if \(Y\) is affine.
Cf. Ind-scheme.
Referenced: Affine grassmannian.
TODO Luna’s slice theorem
TODO McKay correspondence
TODO Minimal model
Referenced: Castelnuovo theorem.
Minuscule
A coweight \(\mu\) is minuscule if \[\langle \alpha, \mu \rangle \leq 1\] for all \(\alpha\) positive. For minuscule \(\mu\), we have \({\rm Gr}_{\mu} = \overline{{\rm Gr}_{\mu}} = G/P_{\mu}\), where \(P_{\mu}\) is a partial flag.
TODO Moduli space of curves
Referenced: Canonical line bundle.
Canonical line bundle
We now consider the canonical line bundles on \(M_{g,n}\). We consider \(T_{i}^{* } \to \bar{M}_{g,n}\) the line bundle determined by the cotangent space at the \(i\)th point and denoted by \(\mathbb{L}_{i}\). We have geometric result on the canonical line bundles
\(\mathbb{L}_{i}\) is nef on \(\bar{M}_{g,n}\).
We will use the standard notation \(\psi_{i} = c_{1}(\mathbb{L}_{i}) \in H^{2}(\bar{M}_{g,n})\).
For the forgetful map \[\pi: \bar{M}_{g,n + 1} \to \bar{M}_{g,n}\] we define \(k_{r} = \pi_{* } \psi_{n + 1}^{r + 1} \in H^{2r}(\bar{M}_{g,n})\). Under these assumptions, we have
\(H^{2}(M_{g,n}, \mathbb{Q}) \cong \pic(M_{g,n}, \mathbb{Q})\) is generated by \(k_{1}, \psi_{1}, \cdots, \psi_{n}\).
Referenced: Descent integral.
Descent integral
Following the terminology in Canonical line bundle. We define \[\langle \tau_{1}^{k_{1}} \cdots \tau_{n}^{k_{n}} \rangle_{g,n} = \int_{\bar{M}_{g,n}} \psi_{1}^{k_{1}} \cdots \psi_{n}^{k_{n}}\] Here, we must make sure \(\sum k_{i} = 3g - 3 + n\) and \(2g - 2 + n \leq 0\). Or by simplify notation, we make \(n = \sum_{k_{i}} - 3g + 3\). These integrals are called descent integral.
Referenced: Witten’s Conjecture.
Witten’s Conjecture
Considering the Descent integrals, we have generating function \[F_{g}(t_{0}, t_{1}, t_{2}, \cdots) = \sum_{\{n_{i}\}} \prod_{i = 1}^{n} \frac{t_{i}^{n_{i}}}{n_{i}!} \langle \tau_{0}^{n_{0}}\tau_{1}^{n_{1}} \cdots \rangle_{g}\] where the sum on right hand side is by sum over sequences with only finitely many nonzero terms. It can also be written as \(F_{g} = \sum_{n = 0}^{\infty} \frac{\langle \phi^{n} \rangle_{g}}{n!}\), where \(\phi = \sum_{i = 0}^{\infty} t_{i} \tau_{i}\). \(F_{g}\) is the generating function that contains all integrals of \(\psi\) classes over all moduli spaces \(\bar{M}_{g,n}\).
We can put all data for all genera together by defining \[F(\lambda, t) = \sum_{g = 0}^{\infty} \lambda^{2g - 2} F_{g}\] We introduce another notation \[\langle \langle \tau_{k_{1}} \cdots \tau_{k_{n}} \rangle \rangle = \frac{\partial}{\partial t_{k_{1}}} \cdots \frac{\partial}{\partial t_{k_{n}}} F\]
We have following Witten’s conjecture and Kontsevich’s theorem
For \(n \geq 1\), we have \[(2n + 1) \lambda^{-2} \langle \langle \tau_{n} \tau_{0}^{2} \rangle \rangle = \langle \langle \tau_{n - 1} \tau_{0} \rangle \rangle \langle \langle \tau_{0}^{3} \rangle \rangle + 2 \langle \langle \tau_{n - 1} \tau_{0}^{2} \rangle \rangle \langle \langle \tau_{0}^{2} \rangle \rangle + \frac{1}{4} \langle \langle \tau_{n - 1} \tau_{0}^{4} \rangle \rangle\]
By taking \(U = \frac{\partial^{2} F}{\partial t_{0}^{2}}\) and setting \(n = 1\), we have KdV equation \[\frac{\partial U}{\partial t_{1}} = U \frac{\partial U}{\partial t_{0}} + \frac{1}{12} \frac{\partial^{3} U}{\partial t_{0}^{3}}\]
Referenced: Virasoro constraint.
TODO String equation
TODO Diliton equation
Virasoro constraint
Using the same generating function as in Witten’s Conjecture. We define partition function \(Z(\lambda, t) = \exp(F)\). Now we define a sequence of operators satisfying the Virasoro bracket. \[L_{n} = -\frac{(2n + 3)!!}{2 ^{n + 1}} \frac{\partial}{\partial t_{n + 1}} + \sum_{i = 0}^{\infty} \frac{(2i + 2n + 1)!!}{(2i - 1)!! 2 ^{n + 1}} t_{i} \frac{\partial}{\partial t_{i + n}} + \frac{\lambda^{2}}{2} \sum_{i = 0}^{n - 1} \frac{(2i + 1)!! (-2i +2n - 1)!!}{2 ^{n + 1}} \frac{\partial^{2}}{\partial t_{i} \partial t_{n - 1 - i}}\] Then we have that \[L_{n}(Z) = 0\] for \(n \geq -1\), which is called Virasoro constraint.
Moduli space of Stable Maps
Let \(X\) be a non-singular projective variety. A morphism \(f\) from a pointed nodal curve to \(X\) is a stable map if every genus \(0\) contracted component of \(\Sigma\) has at least three special points, and every genus \(1\) contracted component has at least one special point.
A stable map represents a homology class \(\beta \in H_{2}(X, \mathbb{Z})\) if \(f_{*}[C] = \beta\).
The moduli space of stable maps from \(n\)-pointed genus \(g\) nodal curves to \(X\) representing the class \(\beta\) is denoted \(\bar{M}_{g,n}(X, \beta)\). The subscript \(n\) may be omitted if \(n = 0\).
The moduli space \(\overline{M}_{g,n}(X, \beta)\) is a Deligne-Mumford stack. And the moduli space admits Virtual fundamental class.
Referenced: Gromov-Witten theory.
Morphism
Referenced: Toric.
Étale
A morphism \(f: X \to Y\) is étale if one of the followings are satisfied
\(f\) is flat and unramified, that is for \(y \in Y\) scheme theoretic fiber \(X_{y}\) is isomorphic to a disjoint union of \(\spec K_{i}\) where \(K_{i}\) is separable field extension of \(\kappa(y)\).
\(f\) is flat and \(\Omega_{X/Y} = 0\).
For any surjection \(A \to A_{0}\) of rings with nilpotent kernel the following commutative diagram can be filled.
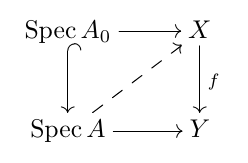
For every point \(x \in X\), there exist affine open neighborhoods \(\spec B\) of \(f(x)\) and \(\spec A \subset f^{-1}(\spec B)\) of \(x\) and an \(A\)-algebra isomorphism \[B \cong (A[x_{1}, \cdots, x_{n}]/(f_{1}, \cdots, f_{n}))_{g}\] for some \(f_{1}, \cdots, f_{n}, g \in A[x_{1}, \cdots, x_{n}]\) such that determinant \(\det(\frac{\dif f_{j}}{\dif x_{i}})_{1 \leq i,j \leq n} \in B\) is a unit.
In addition \(X\) and \(Y\) are locally of finite type over an algebraic closed field \(K\), then above is equivalent to
- For all \\(x\\) closed point, the induced map \\(\hat{\mathcal{O}}\_{Y, f(x)} \to \hat{\mathcal{O}}\_{X, x}\\) on completions is an isomorphism.
- If \\(X\\) and \\(Y\\) are smooth, the induced map \\(T\_{X,x} \to T\_{Y,f(x)}\\) on tangent spaces is an isomorphism.
A morphism is called étale at \(x\) if it is étale in a small neighborhood.
Toric
Let \(V_{i} = \spec (\CC[S_{i}])\) be the Affine toric variety coming from the affine semigroup \(S_{i}\), \(i = 1,2\). Then a Morphism \(\phi: V_{1} \to V_{2}\) is toric if the corresponding map of coordinate rings \(\phi^{* }: \CC[S_{2}] \to \CC[S_{1}]\) is induced by a Semigroup homomorphism \(\hat{\phi}: S_{2} \to S_{1}\).
A toric morphism is equivariant. That is \[\phi(t \cdot p) = \phi(t) \cdot \phi(p)\] for \(t \in T_{N}\) and \(p \in V_{1}\).
For Algebraic stack, a morphsim \(X \to Y\) is unramified or étale if \(X \to Y\) is representable by Deligne-Mumford stack and has the corresponding property.
Non-normal toric variety
Toric variety is not necessarily normal. For example, \(\spec \CC[x,y]/(x^{2} - y^{3})\).
Polyhedral cone
A convex polyhedral cone in a real vector space \(N_{\RR}\) is a set of the form \[\sigma = \cone(S) = \{\sum_{u \in S} \lambda_{u} u \mid \lambda_{u} \geq 0\}\] where \(S \subset N_{\RR}\) is finite. And we say that \(\sigma\) is generated by \(S\). In particular, we define \(\cone(\emptyset) = \{0\}\).
The dimension of polyhedral cone is the dimension of the minimal linear space containing the cone.
Referenced: Affine toric variety, Polytope, Dual cone, Supporting hyperplane, Face, Dual face, Relative interior space, Strongly convex, Separation lemma, Rational, Smooth, Simplicial, Saturated.
Polytope
A polytope in \(N_{\RR}\) is a set of the form \[P = \conv(S) = \{\sum_{u \in S} \lambda_{u}u \mid \lambda_{u} \geq 0, \sum_{u \in S} \lambda_{u} = 1\}\] where \(S \subset N_{\RR}\) is finite. We say that \(P\) is the convex hull of \(S\).
Cf. Polyhedral cone.
Dual cone
Given a Polyhedral cone \(\sigma \in N_{\RR}\), we have a dual cone in dual space \(M_{\RR}\) of \(N_{RR}\), \[\sigma^{\vee} = \{m \in M_{\RR} \mid \langle m, n \rangle \geq 0 \text{ for all } u \in \sigma\}\]
Obviously, we have \((\sigma^{\vee})^{\vee} = \sigma\).
Supporting hyperplane
For \(m \in M_{\RR}\), the dual space of \(N_{\RR}\), We define \(H_{m} = \{u \in N_{\RR} \mid \langle m,n \rangle = 0\}\), and \(H_{m}^{+ } = \{u \in N_{\RR} \mid \langle m, n \rangle \geq 0\}\). We call \(H_{m}\) a supporting hyperplane of a Polyhedral cone \(\sigma\) if we have \(\sigma \subset H_{m}^{+}\) and \(H_{m}^{ +}\) is then called supporting half-space.
Referenced: Face, Separation lemma.
Face
A face of a cone of the Polyhedral cone \(\sigma\) is \(\tau = H_{m} \cap \sigma\) for some \(m \in \sigma^{\vee}\) and \(H_{m}\) is the Supporting hyperplane. We may write as \(\tau \preceq \sigma\). If \(\tau \neq \sigma\), we called \(\tau\) the proper face and write \(\tau \prec \sigma\). A facet is a face of codimension \(1\) and an edge is a face of dimension \(1\).
The faces of the Strongly convex Rational Polyhedral cone gives affine open subset of the Affine toric variety. ([CLS2011] Proposition 1.3.16)
Let \(\tau\) be a face of strongly convex rational polyhedral cone \(\sigma\) and \(\tau = H_{m} \cap \sigma\) for some \(m \in \sigma^{\vee} \cap M\). Then we have \[\CC[S_{\tau}] = \CC[S_{\sigma}]_{\chi^{m}}\]
Referenced: Dual face.
Dual face
Given a Face \(\tau \preceq \sigma\), we have \[\tau^{\perp} = \{m \in M_{\RR} \mid \langle m,n \rangle = 0 \text{ for all } u \in \tau\}\] and the dual face is defined as \[\tau^{* } = \sigma^{\vee} \cap \tau^{\perp}\]
Cf. Polyhedral cone.
Relative interior space
The relative interior space of a Polyhedral cone \(\sigma\) is the interior of the cone with respect to the minimal linear space containing it. The terminology is useful, since we may consider the cone with less dimension than the ambient linear space.
Strongly convex
A Polyhedral cone is called strongly convex if the origin is a face of the cone. Or equivalently speaking we have \(\sigma \cap (- \sigma) = \{0\}\).
Referenced: Affine toric variety, Face, Smooth, Simplicial, Saturated.
Separation lemma
Let \(\sigma_{1}, \sigma_{2}\) be polyhedral cones in \(N_{\RR}\), and they meet along a common face \(\tau = \sigma_{1} \cap \sigma_{2}\). Then we have \[\tau = H_{m} \cap \sigma_{1} = H_{m} \cap \sigma_{2}\] for some \(m\) in the dual space of \(N_{\RR}\).
Cf. Supporting hyperplane, Polyhedral cone.
Rational
A Polyhedral cone is called rational if by equating \(N_{\RR} = N \otimes_{\ZZ} \RR\), where \(N\) is a Lattice, we have \(\sigma = \cone(S)\) for \(S \in N\).
For rational cone, \(\rho \subset \sigma\) an edge, the generator of \(\rho \cap N\) is called ray generator of \(\rho\).
Referenced: Affine toric variety, Face, Smooth, Simplicial, Saturated.
Smooth
A Strongly convex, Rational Polyhedral cone is called smooth or regular if its minimal generators form part of a \(\ZZ\)-basis of \(N\).
The following theorem justify the above name. ([CLS2011] Theorem 1.3.12)
Let \(\sigma \subset N_{\RR}\) be a strongly convex rational polyhedral cone. Then \(U_{\sigma}\) is smooth if and only if \(\sigma\) is smooth. Furthermore, all smooth affine varieties are of this form.
Simplicial
A Strongly convex, Rational Polyhedral cone is called simplicial if its minimal generators are linearly independent over \(\RR\).
Predeformation functor
A predeformation functor is a covariant functor \(F: \cat{Art}(\Lambda, k) \to \cat{Set}\) such that \(F(k)\) is the one-element set. The tangent space \(T_{F}\) is defined to be \(F(k[\epsilon]/(\epsilon^{2}))\). The objects of \(\cat{Art}(\Lambda, k)\) are local Artin \(\Lambda\)-algebra with residue field \(k\).
Cf. Tangent space.
Referenced: Deformation functor, Hull, Schlessinger’s theorem.
Presheaf
A presheaf on a category \(C\) is a functor \[F: C^{op} \to \cat{Set}\] We usually write \(\hat{C}\) for teh category of presheaves on \(C\).
Separated
A Presheaf \(F\) on \(C\) is called separated if for every \(U \in C\) and \(\{U_{i} \to U\}_{i \in I} \in \cat{Cov}(U)\) the map \(F(U) \to \prod F(U_{i})\) is injective.
Prestack
A prestack over \(\cat{Sch}\) is a category \(\mathfrak{X}\) together with functor \(p: \mathfrak{X} \to \cat{Sch}\) such that
for any diagram
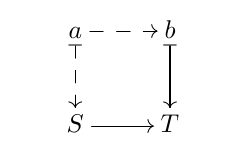
there exist a morphism \(a \to b\) over \(S \to T\).
for any diagram
there exists a unique arrow \(a \to b\) over \(R \to S\) filling in the diagram.
Presheaves are prestacks.
Cf. Presheaf.
Schemes are prestacks.
A morphism of prestacks \(f: \mathfrak{X} \to \mathfrak{Y}\) is a functor commutes with morphism to \(S\). For \(f,g\) two morphisms, a 2-morphism is a natural transformation \(\alpha: f \to g\) such that \(\alpha_{a}: f(a) \to g(a)\) in \(\mathfrak{Y}\) is over \(\id_{s}\).
Prorepresnetable
Let \(\widehat{\cat{Art}(\Lambda, k)}\) be the category of complete Noetherian local \(\Lambda\)-algebra with residue field \(k\). Set \(\hat{F} := \varprojlim_{n} F(R/ \mathfrak{m}^{n})\). We say that \(F\) is propresentable if and only if \(\hat{F}\) is representable.
Referenced: Schlessinger’s theorem.
Pure
\(E\) is pure of dimension \(d\) if \(\dim F = d\) for all non-trivial coherent subsheaves \(F \subset E\).
Referenced: Stable.
Rational surface
A rational surface is an algebraic surface birational equivalent to \(\CC P^{2}\).
Reflexive
A coherent sheaf \(E\) of codimension \(c\) is called reflexive if \(\theta_{E}: E \to E^{DD}\) is an isomorphism. \(E^{DD}\) is called the reflexive hull of \(E\).
Cf. Dual sheaf.
Regular sequence
Let \(M\) be a module over a local ring \(A\). An element \(a \in \mathfrak{m}\) of \(A\) is called \(M\)-regular if \(m \to am\) is injective morphism. A sequence \(a_{1}, \cdots, a_{l} \in \mathfrak{m}\) is a \(M\)-regular sequence if \(a_{i}\) is \(M/(a_{1}, \cdots, a_{i - 1}) M\) regular for all \(i\).
The definition can be generalized to sheaf theoretic language. Let \(X\) be a Noetherian scheme, let \(E\) be a coherent sheaf on \(X\) and \(L\) a line bundle on \(X\). A section \(s \in H^{0}(X, L)\) is called \(E\)-regular if and only if \(E \otimes L^{\vee} \stackrel{\cdot s}{\to} E\) is injective. A sequence \(s_{1}, \cdots, s_{l} \in H^{0}(X, L)\) is called \(E\)-regular similarly in the module theoretic language.
Referenced: Depth.
Residual gerbe
Let \(X\) be an Algebraic stack and \(x \in \abs{X}\) be a point. Choose a smooth presentation \((U, u) \to (X, x)\). The residual gerbe of \(x\) is the substack \(G_{x} \subset X\) defined as the stackification of the full subcategory \(G_{x}^{pre}\) consisting of object \(a \in X\) over \(S\) which factor as \(a: S \to \spec \kappa(u) \to X\).
TODO Riemann-Roch theorem
TODO Ring
TODO Local ring
Complete
A Local ring is called complete if it is complete with respect to the \(\mathfrak{m}\)-adic topology.
Referenced: Hull.
TODO Noetherian
Referenced: Hull.
Schlessinger’s theorem
The Schlessinger’s theorem is a criterion for existence of Hull or Prorepresnetibility.
Let \(F\) be a predoformation functor. Then \(F\) has a hull if and only if the following conditions (1-3) holds, and \(F\) is prorepresentable if and only if in addition (4) holds.
- The map \[F(A' \times_{A} A'') \to F(A') \times_{F(A)} F(A'')\] is surjective when \(A'' \to A\) is a small thickening.
- The above map is bijective when \(A = k\) and \(A'' = k[\epsilon]\).
- The tangent space \(T_{F}\) is finite-dimensional over \(k\).
- The above map is bijective if \(A'' = A'\) and \(A' \to A\) is a small thickening.
Cf. Predeformation functor, Small thickening.
Referenced: Deformation functor.
Semigroup
Referenced: Toric, Affine semigroup, Irreducible.
Affine semigroup
An affine semigroup is a Semigroup where the binary operation is commutative, finite generated, and can be embedded in a Lattice \(M\).
Referenced: Affine toric variety, Pointed, Saturated.
Irreducible
An element in a Semigroup is called irreducible if \(m = m' + m''\) in the semigroup, then we have \(m' = 0\) or \(m'' = 0\).
Pointed
A pointed affine semigroup \(S\) is the Affine semigroup such that \(S \cap (-S) = \{0\}\).
The pointed affine semigroup is related to Affine toric variety by the following proposition.
If we write \(V = \spec(\CC[S])\), then the torus action has a fixed point if and only if \(S\) is pointed. What’s more, the fixed point is unique and given by semigroup homomorphism \(\phi:S \to \CC\) defined by
\begin{equation} m \to \begin{cases} 1 & m = 0 \\ 0 & m \neq 0 \end{cases} \end{equation}
Saturated
An Affine semigroup \(S \subset M\) is saturated if for all \(k \in \NN \backslash \{0\}\) and \(m \in M\), \(km \in S\) implies \(m \in S\). ([CLS2011] p.37)
One important source of the saturated affine semigroup is \(S_{\sigma} = \sigma^{\vee} \cap M\) where \(\sigma\) is a Strongly convex Rational Polyhedral cone.
The saturated affine semigroup is related to normal Affine toric variety. ([CLS2011] Theorem 1.3.5)
Let \(V\) be an affine toric variety with torus \(T_{N}\). Then \(V\) is normal if and only if \(V = \spec(\CC[S])\), where \(S \subset M\) is a saturated affine semigroup.
TODO Semismall map
Referenced: Small map.
TODO Serre duality
Sheaf
A Presheaf \(F\) on \(C\) is called a sheaf if for every object \(U \in C\) and covering \(\{U_{i} \to U\}\) the sequence \[F(U) \to \prod_{i} F(U_{i}) \rightrightarrows \prod_{i,j} F(U_{i} \times_{U} U_{j})\] is exact, where the two maps on the right are induced by the two projections \(U_{i} \times_{U} U_{j} \to U_{i}\) and \(U_{i} \times U_{j} \to U_{j}\). Here exact means equalizer.
We write \(C^{~}\) for the category of sheaves on \(C\).
Let \(C\) be a site. The inclusion \[\text{(sheaves on \(C\))} \hookrightarrow \text{(presheaves on \(C\))}\] has a left adjoint \(F \to F^{a}\).
Cf. Site.
The left adjoint \(F \to F^{a}\) is called sheafification and \(F^{a}\) is called the sheaf associated to \(F\).
For \(f: C' \to C\) functor between small categories, we have functor \(f_{*}: \hat{C} \to \hat{C}\) by \((f_{*}F)(X) := F(f(X))\). And we have left adjoint functor \(\hat{f}^{*}\). And if \(f\) is Continuous, then the induced functor between Topoi \(f_{*}: T \to T'\) also has a left adjoint.
If finite limits in \(C'\) are representable and that \(f\) commutes with all finite limits in \(C'\). Then \(f^{*}\) commutes with finite limits and hence \(f\) defines a morphism of topoi.
Referenced: Framed moduli space, Sheafification, Topos.
Euler characteristic
The Euler characteristic of a sheaf \(E\) is \[\chi(E) = \sum (-1)^{i} h^{i}(X, E)\]
Hilbert polynomial
The Hilbert polynomial is the function \[P(E,m): m \to \chi(E \otimes \OO(m))\]
For Hilbert polynomial \(P(E, m) = \sum_{i = 0}^{\dim(E)} \alpha_{i}(E) \frac{m^{i}}{i!}\), we define reduced Hilbert polynomial as \[p(E)= P(E)/ \alpha_{d}(E) \]
Referenced: Multiplicity, Rank, Stable, μ-stable.
Multiplicity
For Hilbert polynomial \(P(E, m) = \sum_{i = 0}^{\dim(E)} \alpha_{i}(E) \frac{m^{i}}{i!}\), and \(E \neq 0\), the leading coefficient \(\alpha_{\dim(E)}(E)\) is called multiplicity.
Rank
For Hilbert polynomial \(P(E, m) = \sum_{i = 0}^{\dim(E)} \alpha_{i}(E) \frac{m^{i}}{i!}\), and \(\dim(E) = \dim(X) = d\), \[\rk(E) := \frac{\alpha_{d}(E)}{\alpha_{d}(\OO_{X})}\]
Stable
We write \(p_{1} \leq p_{2}\) for two polynomials if \(p_{1}(x) \leq p_{2}(x)\) when \(x \gg 0\).
A coherent sheaf \(E\) of dimension \(d\) is semistable if \(E\) is Pure and for any proper subsheaf \(F \subset E\), one has Hilbert polynomial \(p(F) \leq p(E)\). And is stable if \(E\) is semistable and \(p(F) < p(E)\)
Let \(F\) and \(G\) be semistable purely \(d\)-dimensional sheaves. If \(p(F) \geq p(G)\) then \(\Hom(F, G) = 0\). If \(p(F) = p(G)\) and \(f: F \to G\) non-trivial, then \(f\) is injective if \(F\) is stable and surjective if \(G\) is stable. If \(p(F) = p(G)\) and \(\alpha_{d}(F) = \alpha_{d}(G)\) then any non-trivial homomorphism \(f: F \to G\) is an isomorphism provided \(F\) or \(G\) is stable.
If \(E\) is a stable sheaf, then \(\End(E)\) is a finite dimensional division algebra over \(k\). In particular if \(k\) is algebraically closed, then \(\End(E) \cong k\).
Referenced: Geometrically stable.
Geometrically stable
A coherent sheaf \(E\) is geometrically stable if for any base field extension \(X_{K} = X \times_{k} \spec(K) \to K\) the pull-back \(E \otimes_{k} K\) is Stable.
μ-stable
Let \(E\) a coherent sheaf of dimension \(d = \dim X\) with Hilbert polynomial \(P(E, m) = \sum_{i = 0}^{\dim(E)} \alpha_{i}(E) \frac{m^{i}}{i!}\). We define the degree of \(E\) by \[\deg(E) := \alpha_{d - 1}(E) - \rk(E) \cdot \alpha_{d - 1}(\OO_{X})\] and its slope by \[\mu(E) := \frac{\deg(E)}{\rk(E)}\]
A coherent sheaf \(E\) of dimension \(d\) is \(\mu\)-(semi)stable if \(T_{d - 2}(E) = T_{d - 1}E\) and \(\mu(F)(\leq)\mu(E)\) for all subsheaves \(F \subset E\) with \(0 < \rk(F) < \rk(E)\).
\(E\) is \(\mu\)-stable \(\Rightarrow\) \(E\) is stable \(\Rightarrow\) \(E\) is semistable \(\Rightarrow\) \(E\) is \(\mu\)-semistable.
Sheafification
Cf. Sheaf.
Simple resolution
See [nakajima1999] p.47.
A simple singularity is a quotient space \(\CC^{2} / \Gamma\), where \(\Gamma\) is a finite subgroup of \(\SU(2)\). A simple resolution is a resolution of simple singularity.
The following theorem construct the simple resolution by Hilbert scheme of points.
Consider the Hilbert scheme \((\CC^{2})^{ [N]}\) where \(N\) is the order of \(\Gamma\). The \(\Gamma\) orbit of a point \(p\) in \(\CC\backslash \{0\}\) defines a \(0\) dimensional subscheme \(Z \in (\CC^{2})^{ [N]}\). Let \(X\) be the component of \(\Gamma\) fixed point set which contains the set of \(\Gamma\)-orbits \(\Gamma \cdot (\CC \backslash \{0\})\). Then we have that the restriction of the Hilbert-Chow morphism to \(X\) is the minimal resolution of singularities of \(\CC^{2} \backslash \Gamma \cong (S^{N}(\CC^{2}))^{\Gamma}\).
Referenced: Simple singularity.
Simple singularity
See Simple resolution.
Site
A category with a Grothendieck topology is called a site.
Let \(X\) be a topological space, \(\cat{Op}(X)\) the category of open sets. Then let \(\cat{Cov}(U)\) to be the collections \(\{U_{i} \to U\}\) for which \(U = \cup U_{i}\), where \(U_{i}\) is a Grothendieck topology. For Zariski topology space, it is called small Zariski site.
Let \(X\) be a scheme and let \(\cat{(Sch/X)}\) be the category of \(X\)-schemes. We define \(\cat{Cov}(X)\) be the set of collections \(\{U_{i} \to U\}\) of \(X\)-morphisms for which each morphism \(U_{i} \to U\) is étale and the map \[\coprod U_{i} \to U\] is surjective. It is called big étale site.
Similarly, we can define fppf site (flat and locally of finite presentation) and smooth site.
Referenced: Continuous, Étale site, Fppf site, Sheaf, Smooth site, Topos.
TODO Small map
See Semismall map.
Small thickening
A surjective map \(f: A \to B\) in \(\cat{Art}(\Lambda, k)\) is a small thickening if \(\ker f \mathfrak{m}_{A} = 0\) and \(\ker f\) is principal.
Referenced: Schlessinger’s theorem.
Smooth
Let \(F, F': \cat{Art}(\Lambda, k) \to \cat{Set}\) be covariant functors, with a morphism \(\phi: F \to F'\). We say that \(\phi\) is smooth if for every surjection \(A \to B\) in \(\cat{Art}(\Lambda, k)\) the map \[F(A) \to F(B) \times_{F'(B)}F'(A)\] is surjective.
Smoothness of Hilbert scheme
See [nakajima1999], Section 1.3.
Suppose \(X\) is nonsingular of dimension \(2\), then \(X^{ [n]}\) is nonsingular of dimension \(2n\) and the Hilbert-Chow morphism is a resolution of singularities.
Cf. Hilbert scheme, Hilbert-Chow morphism.
Smooth site
See Site.
TODO Spectral sequence
Referenced: Eilenberg-Zilber theorem.
TODO Beilison spectral sequence
Splitting torus
A splitting torus is a torus of type \(k^{\times n}\).
Cf. Torus.
Stabilizer
If \(X\) is an Algebraic stack and \(x: \spec K \to X\) is a field-valued point, the stabilizer of \(x\) is defined as the group scheme \(G_{x} = Aut_{X(K)}(x)\).
By representability of the diagonal, \(G_{x}\) is a group algebraic space.
If \(X\) is a Deligne-Mumford stack and \(x \in \abs{X}\), we define the geometric stabilizer of \(x\) as the discrete group \(G = G_{\bar{x}}\) where \(\bar{x}: \spec k \to X\) is any representative of \(x\) with \(k\) algebraic closed.
Stack
A Prestack \(\mathfrak{X}\) over a Site \(\mathfrak{S}\) is a stack if the following conditions hold for all coverings \(\{S_{i} \to S\}\) of an object \(S \in \mathfrak{S}\):
- For object \(a\) and \(b\) in \(\mathfrak{X}\) over \(S\) and morphism \(\phi_{i}: a|_{S_{i}} \to b\) such that \(\phi_{i}|_{S_{ij}} = \phi_{j}|_{S_{ij}}\), there exists a unique morphism \(\phi: a \to b\) with \(\phi|_{S_{i}} = \phi_{i}\).
- For objects \(a_{i}\) over \(S_{i}\) and isomoprhisms \(\alpha_{ij}: \alpha_{i}|_{S_{ij}} \to \alpha_{j}|_{S_{ij}}\) satisfying \(\alpha_{ij}|_{S_{ijk}} \circ \alpha_{jk}|_{S_{ijk}} = \alpha_{ik}|_{S_{ijk}}\) on \(S_{ijk}\), then there exists an object \(a\) over \(S\) and isomorphisms \(\phi_{i}: a|_{S_{i}} \to a_{i}\) such that \(\alpha_{ij} \circ \phi_{i}|_{S_{ij}} = \phi_{j}|_{S_{ij}}\) on \(S_{ij}\).
If \(g \geq 2\), then \(\mathcal{M}_{g}\) is a stack over \(\cat{Sch}_{Ét}\).
For all integers \(r,d\) with \(r \geq 0\), \(Bun_{r,d}( C)\) is a stack over \(\cat{Sch/ \CC}_{Ét}\).
If \(\mathfrak{X}\) is a prestack over a site \(\mathfrak{S}\), there exists a stack \(\mathfrak{X}^{st}\), which we call the stackfication, and a morphism \(\mathfrak{X} \to \mathfrak{X}^{st}\) of prestacks such that for any stack \(\mathfrak{Y}\) over \(\mathfrak{S}\), the induced functor \(\cat{MOR}(\mathfrak{X}^{st}, \mathfrak{Y}) \to \cat{MOR}(\mathfrak{X}, \mathfrak{Y})\) is an equivalence of categories.
Symmetric power of P^1
Fact, \(S^{n}(\PP^{1}) = \PP^{n}\).
TODO Symplectic resolution
Symplectic structure of Hilbert scheme
See [nakajima1999], Section 1.4.
Suppose \(X\) has a holomorphic symplectic form \(\omega\). Then \(X^{ [n]}\) also has a holomorphic symplectic form.
Cf. Symplectic manifold, Hilbert scheme.
Topos
A topos is a category \(T\) equivalent to the category of Sheaves of sets on Site.
Let \(T\) be a topos, and let \(F: I \to T\) be a functor with \(I\) small. Then the limit \(\varprojlim F\) is representable.
Usually topos is more important than site, as different site can give the same topos.
A morphism of topoi \(f: T \to T'\) is an adjoint pair \[f = (f^{* }, f_{* }, \phi)\] where \[f_{* }: T \to T', \quad f^{* }: T' \to T\] are functors and \(\phi\) is an isomorphism \[\phi: \Hom_{T}(f^{* }(-), -) \to \Hom_{T'}(-, f_{* }(-))\] of bifunctors and \(f^{* }\) commutes with finite limits.
Referenced: Continuous, Category of modules, Sheaf, Ringed, Point.
Ringed
A ringed Topos is a pair \((T, \Lambda)\), where \(\Lambda\) is a ring object in topos \(T\). A morphism between ringed topoi is a pair \((f, f^{\shar})\) consisting of a morphism of topoi \(f: T \to T'\) and a morphism of rings in \(T'\) \(f^{\shar}: \Lambda' \to f_{*} \Lambda\).
Point
Let \(\text{pt}\) denote the Topos of sheaves on the one-point space. A point of the topos \(T\) is a morphism of topoi \[x: \text{pt} \to T\] We say that the topos \(T\) has enough points if there exists a set of points \[\{x_{i}: \text{pt} \to T\}\] such that the induced functor \[T \to \cat{Set}^{I}, F \to \{x_{i}^{*}F\}\] is faithful.
Toric ideal
A prime Lattice ideal is called toric ideal.
We have following criterion for toric ideal.
An ideal \(I \subset \CC[x_{1}, \cdots, x_{s}]\) is toric if and only if it is prime and generated by binomials.
Referenced: Affine toric variety.
TODO Toric variety
The toric variety is a field connecting algebraic geometry, combinatorial and mathematical physics. Our main reference is [CLS2011].
Referenced: Non-normal toric variety.
Torsion filtration
The torsion filtration of a coherent sheaf \(E\) is the unique filtration \[0 \subset T_{0}(E) \subset \cdots \subset T_{d}(E) = E\] where \(d = \dim(E)\) and \(T_{i}(E)\) is the maximal subsheaf of \(E\) of dimension \(\geq i\).
Torsion free
A coherent sheaf \(E\) is called torsion free if for each \(x \in X\) and \(s \in \OO_{X,x} \backslash \{0\}\) the multiplication by \(s\) induces a injective morphism \(E_{x} \to E_{x}\).
Torsor
Let \(S\) be a Site and \(G\) a sheaf of groups on \(S\). A \(G\)- torsor on \(S\) is a sheaf \(P\) of sets on \(S\) with left action \(\sigma: G \times P \to P\) of \(G\) such that
- For every object \(X \in S\), there exists a covering \(\{X_{i} \to X\}\) such that \(P(X_{i}) \neq 0\), and
- The action map \((\sigma, p_{2}): G \times P \to P \times P\) is an isomorphism.
Torus
Over \(\CC\), a torus is \(\CC^{* n}\). In general a scheme \(X\) over \(k\) is called a torus if \(X_{k^{a}}\) is of the form \((k^{a})^{\times n}\) where \(k^{a}\) is the algbraic closure of \(k\).
The following proposition is useful in toric geometry over \(\CC\). The image of a torus in a torus is also a torus.
Let \(T_{1}\) and \(T_{2}\) be tori, and \(\Phi: T_{1} \to T_{2}\) a group homomorphism and morphism of varieties. Then the image of \(\Phi\) is a torus and closed in \(T_{2}\).
A group subvariety of a torus is a torus.
If \(H \subset T\) is an irreducible group subvariety of \(T\). Then \(H\) is a torus.
Referenced: Affine toric variety, Character (of a torus), Splitting torus.
Unramified
See Étale.
Versal extension
An \(A\)-Extension \((P, f)\) is called versal if for every other \(A\)-extensions \((R', \phi)\) of \(R\), there exists a homomorphism of extensions \(r: (P, f) \to (R, \phi)\). For example, for \(R = P/I\) where \(P\) a polynomial ring over \(A\), \[0 \to I/I^{2} \to P/I^{2} \to R \to 0\] is a versal \(A\)-extension of \(R\).
The word versal is similar to universal and certainly has some similarities. However, I don’t know which words come into math world first.
Virasoro bracket
Virasoro bracket is a set of commutator relation for operators \(L_{n}\) such that \[[L_{n}, L_{m}] = (n - m) L_{n + m}\]
Referenced: Virasoro constraint.
TODO Virtual fundamental class
The analog of Fundamental class for stacks and orbifold.
Referenced: Donaldson-Thomas theory, Moduli space of Stable Maps.
TODO Yoneda product
Symplectic Geometry
Liouville vector field
Let \((M, \omega)\) is a Symplectic manifold. A vector field \(V: M \to TM\) is Liouville if \(L_{X} \omega = \omega\). Cf. Lie derivative.
The existence of a Liouville vector field implies that \((M, \omega)\) is exact as the one-form \(\lambda = i_{V} \omega\) satisfies that \(\dif \lambda = \omega\).
Referenced: Weinstein manifold.
Symplectic manifold
A symplectic manifold is a smooth Manifold \(X\) of even dimension \(\dim X = 2n\), equipped with a symplectic form a closed smooth \(2\)-form \(\omega \in \Omega_{cl}^{2}(X)\) such that \(\omega\) is non-degenerate. That is \(\omega^{n}\) has the maximal rank at every point \(p\), or equivalently that \((\wedge^{2} T_{p}^{* }X, \omega_{p})\) symplectic vector space for every \(p\).
Referenced: Symplectic structure of Hilbert scheme, Liouville vector field, Weinstein manifold.
Weinstein manifold
A Symplectic manifold \((M, \omega)\) is Weinstein if it comes with a distinguished Liouville vector field \(Y\), and a proper bounded below function \(h: M \to \RR\), such that \(\dif h(Y)\) is positive on a sequence of level set \(h^{-1}(c_{k})\) with \(\lim_{k}c_{k} = \infty\).
A Weinstein manifold is called of finite type if \(\dif h(Y) > 0\) outside a compact subset of \(M\) and is called complete if the flow of \(Y\) is defined for all times.
Geometric representation theory
In geometric representation theory, we tries to encode the algebra operation in geometric objects. The one of the general construction is the usage of correspondence, that is the cycles or sheaves etc in \(X_{1} \times X_{2}\). It is a nonlinear analog of matrices. To retain the linear information, we consider functors such as Equivariant cohomology and Equivariant K-theory.
Langlands dual pair
The Langlands dual is a pair of Algebraic groups \((X, Y)\) such that the root system of \(X\) is coroot of \(Y\) and vice versa. The center of \(X\) is the fundamental group of \(Y\) and vice versa.
For example \((\Sp(n), \SO(2n + 1))\), \((\SO(2n), \SO(2n))\) and \((\SL(n), \PGL(n))\).
Steinberg variety
For a general symplectic resolution \[\pi: X \to X_{0}\] we have the Steinerg variety \(X \times_{X_{0}} X\).
Referenced: Algebraic Geometry.
Geometric Topology
Named geometric topology, this section includes some result in \(4\)-manifold and knot theory and higher dimensional topology.
11/8 conjecture
By Freedman’s classification of topological 4-manifold, Rokhlin Theorem and Donaldson diagonalizable theorem, the only remaining case to determine the existence of smooth structure on topological \(4\)-manifold are those with \(Q_{X}\) even and indefinite. That is \(Q_{X} = mE_{8} \oplus n \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\). Since we have K3 surface with \(Q_{X} = 2E_{8} \oplus 3 \begin{pmatrix}0 & 1\\ 1 & 0 \end{pmatrix}\) and \(S^{2} \times S^{2}\) with \(Q_{X} = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}\), we can show that the for \(Q_{X}\) with \(m = 2k\) and \(n \geq 3k\) the smooth structure on the manifold exists. The conjecture is that that is the only possibility for the existence of smooth structure.
If \(X\) is spin, smooth and \(Q_{X} = 2k E_{8} \oplus n \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}\), then \(n \geq 3k\). Or equivalently speaking \(b_{2}(X) \geq \frac{11}{8} \abs{\sigma(X)}\).
A theorem by Furuta says
Let \(X\) be a spin \(4\)-manifold, such that \(b_{2}(X) \neq 0\). Then \[b_{2}(X) \geq \frac{10}{8} \abs{\sigma(X)} + 2\]
The Seiberg-Witten invariant together with spin Dirac operator can give one proof. The proof suggests Bauer-Furuta invariant.
The current status (2021 Sep.) of the conjecture is that \(k \leq 1\) case is proved. For \(k > 1\), we have \[n \geq 2k + \begin{cases} 2 & k = 1,2,5,6 \\ 3 & k = 3,4,7 \\ 4 & 0 \end{cases} \mod 8 \]
Affine braid group
We define the affine braid group to be \[\tilde{B_{n}} = \langle s_{1}, \cdots, s_{n -1}, t_{1}, \cdots, t_{n}\rangle\] with the same condition as Braid group with addition \[s_{i}t_{i + 1} = t_{i} s_{i}\]
TODO Alexander duality
TODO Alexander polynomial
Referenced: Fintushel-Stern knot surgery.
Anti-self-dual
A \(n\)-form \(w\) on \(2n\) manifold is called self-dual if \(* w = -w\). Cf. Self-dual.
Referenced: Self-dual.
TODO Bauer-Furuta invariant
Referenced: Geometric Topology.
Botany problem of 4-manifold
For \(b^{+} > 1\), \(\pi_{1} = 1\) irrducible case, by theorem of Fintushel-Stern, any such \(X\) admits \(\infty\) smooth structure.
For \(b^{+} = 1\), then \(\CC P^{2} \shar n \overline{\CC P}^{2}\) for \(n \geq 2\) has \(\infty\) smooth structure. \(S^{2} \times S^{2}\) and \(n < 2\) case is unknown.
\(b^{+} = 0\) case is completely unknown.
In each case, we have no method to determine whether all the smooth structures have been found. That is if a manifold is known to have some smooth structure, we don’t know whether they are all of the possible smooth structures.
It is well known that \(S^{7}\) has 28 different differential structures. And those structures are only smooth structures possible. The proof requires h-Cobordism theorem, so the similar methods can not be applied to \(4\)-manifold.
Braid
A braid is the isotopy class of a Geometric braid.
The braids are in bijection with Redemeister classes of diagrams.
Referenced: Pure, Positive, Braid group.
Pure
A Braid is called pure if it connects \(\{x_{0}\} \times \{0\}\) to \(\{x_{i}\} \times \{1\}\).
Referenced: Braid group.
Positive
A Braid is called positive if it is a product of \(\sigma_{i}\) and not \(\sigma_{i}^{-1}\) in braid group. And a braid is quasi-positive if it has the form \(\prod_{k = 1}^{m} w_{k} \sigma_{ik} w_{k}^{-1}\) where \(w_{k}\) is any word in the braid group. A Knot positive (resp. quasi-positive) if it is a completion of a positive (resp. quasi-positive) braid.
Referenced: Quasi-positive, Knots bounds algebraic surface.
Quasi-positive
See Positive.
Referenced: Knots bounds algebraic surface.
Braid diagram
Consider the projection \(\pi: \RR^{2} \times [0,1] \to \RR \times [0,1]\). Then \(\hat{\beta}\) is called generic if \(\pi(\hat{\beta})\) has simple transversal singular points outside of \(\RR \times \{0,1\}\). Such \(\pi(\hat{\beta})\) is called a geometric braid diagram.
A braid diagram is a regular isotopy class of a geometric braid diagram.
Braid group
The Braids form a group called braid group where the composition is given by glueing two embeddings. Obviously, the Pure braids form a subgroup of braid group. The braid group is denoted by \(B_{n}\), and pure braid group by \(P_{n}\).
\(B_{n}\) is generated by elements
with defining relations \[s_{i}s_{i+1}s_{i} = s_{i + 1}s_{i}s_{i + 1},\; i = 1, \cdots, n - 1\] \[s_{i}s_{j} = s_{j}s_{i}, \; \abs{i - j} > 1\]
The braid group can be realized as a Fundamental group of a manifold. Define \(C_{n} = \{x_{1}, \cdots, x_{n} \in \RR^{2} \mid x_{i} \neq x_{j}\}\). Then we have \(\pi_{1}(C_{n}) = P_{n}\). By considering the \(S_{n}\) action on \(C_{n}\), we have that \(B_{n} = \pi_{1}(C_{n}/ S_{n})\).
Referenced: Affine braid group, Hecke-Iwahori algebra, Representation of braids.
Characteristic class for 4-manifold
We may assume that \(X\) is a connected, closed, oriented, smooth \(4\)-manifold. We have a Signature theorem by Hirzebruch.
\[P_{1}(TX)[X] = 3 \sigma(X)\]
Cf. Pontryagin class.
And theorem by Wenjun Wu on Stiefel-Whitney class.
- For all \(\alpha \in H^{2}(X; \ZZ/2)\), we have \(w_{2}(TX) \cup \alpha = \alpha \cup \alpha\)
- \(w_{3}(TX) = \sq^{1}(w_{2}(TX))\), here \(\sq^{1}\) is the square operator.
By above theorem, Freedman’s classification of topological 4-manifold, Donaldson diagonalizable theorem and algebraic classification of bilinear forms, we have
Let \(X\) be a smooth, closed \(4\)-manifold. Then homeomorphism type of \(X\) is determined by \(e(TX), P_{1}(TX)\)and \(w_{2}(TX)\).
However, characteristic class in dimension \(4\) cannot detect exotic phenomenon.
Clasp number
We define the clasp number of \(K\) to be minimal number of double points of the immersed disk in \(D^{4}\) with boundary \(K\) with only transverse double point.
We have \(c_{4}(k) \leq U(K)\) (Unknot number), for we can trade knot for double points. Also, we have \(g_{S}(K) \leq c_{4}(K)\) (Slice genus) since we can trade double points for genus.
Clifford algebra
Let \(H\) be a real vector space. The tensor algebra \(T(H)\) modulo ideal generated by \(\{v \otimes v + \norm{v}^{2}\}\) is called the Clifford algebra.
Referenced: Clifford module.
Clifford module
A Clifford module of Clifford algebra over \(H\) is a Hermitian complex vector space \(V\) equipped with a Clifford multiplication \(\gamma: H \to \End(V)\) such that
- If \(\norm{e} = 1\), then \(\gamma(e)^{2} = -1\).
- If \(e_{1} \perp v_{2}\), then \(\gamma(e_{1}) \cdot \gamma(e_{2}) + \gamma(e_{2}) \cdot \gamma(e_{1}) = 0\).
- \(\gamma(e)^{* } = - \gamma(e)\).
That is a Clifford module is a representation of Clifford algebra.
The irreducible Clifford module is competely identified.
If \(n = 2k\), then there exists a unique finite dimensional irreducible Clifford module \((S, \gamma)\) up to isomoprhism and \(\dim_{\CC} S = 2^{k}\).
If \(n = 2k + 1\), there are exactly two clifford modules \((S, \gamma), (S, - \gamma)\) up to isomoprhism and \(\dim_{\CC} S = 2^{k}\).
Referenced: Dirac operator, Spin^C structure.
Corbordism
Let \(\mathscr{C}\) denote one of the following categories: smooth / topological / piecewise linear category. Let \(M_{0}, M_{1}\) be oriented \(\mathscr{C}\)-manifold. A cobordism \(W\) form \(M_{0}\) to \(M_{1}\) is a \(n + 1\) dimensional \(\mathscr{C}\)-manifold such that \(\partial W = \bar{M_{0}} \coprod M_{1}\).
We can define the cobordism category \(\cat{Cob}_{n}\), where the objects are closed \(n\) dimensional manifolds and the morphisms are isotopic classes of cobordisms.
Referenced: h-Cobordism.
TODO Cork
Critical point
The critical point of \(f: X \to \RR\) is the map \(\dif f_{p}: T_{p}X \to T_{f(p)} \RR\) is trivial. And \(r = f(p)\) is the critical value, otherwise \(r\) is called the regular value.
Cf. Regular point.
Referenced: Non-degenerate, Critical value, Morse inequality.
Non-degenerate
We say \(p\) Critical point non-degenerate if \(\det({\rm Hess} f_{p}) \neq q\). The index of the \(p\) is the number of negative eigenvalues of Hessian of \(f\) at \(p\).
Referenced: Index.
Critical value
See Critical point.
Referenced: Regular value.
Diagram
The image of a generic geometric representative \(\hat{L}\) of Link \(L\) from \(\RR^{3}\) to \(\RR^{2}\) is a diagram of \(L\).
For equivalent class of diagrams, we have the following theorem by Reidemeister.
Equivalence class of diagrams with respect to the local moves
We can also consider the diagram of Framed links in \(\RR^{3}\). And we have equivalence class of regular isotopy class of framed diagrams on \(\RR^{2}\) is given by
Referenced: Skein relations, Unknot number.
Dirac operator
Given a Clifford module \(S\) over \(H\), we define the Dirac operator \(\dirac: C^{\infty}(H, S) \to C^{\infty}(H, S)\) by \[\dirac \phi = \sum_{i = 1}^{n} \gamma(e_{i}) \cdot \frac{\partial \phi}{\partial e_{i}}\]
\(\dirac\) is a self-adjoint operator with \(\dirac^{2} = \Delta\).
On manifold, given a Spin^C connection \(A\), we can also define the Dirac operator \[\dirac_{A} = \rho \circ \nabla_{A}: \Gamma(s) \to \Gamma(s)\] For decomposition \(S = S^{+} \oplus S^{-}\), we have \(\dirac_{A} = \dirac_{A}^{ +} + \dirac_{A}^{-} \)\(\dirac_{A}^{ +}: \Gamma(S^{ +}) \to \Gamma(S^{-})\) and \(\dirac_{A}^{-}: \Gamma(S^{-}) \to \Gamma(S^{ + })\).
On manifolds, the Dirac operator is also self-adjoint. And we call \(\dirac_{A}^{2}\) the Dirac Laplacian. We have \[\dirac_{A}^{2} \phi = \Delta \phi + \rho(F_{A^{\tau}}^{+ }) \phi + \frac{s}{4} \phi\] where \(\Delta\) is the usual Laplacian and \(F_{A^{\tau}}^{+}\) is the Self-dual part of curvature of the connection induced by \(A\) on \(\det(S^{ +})\)
Donaldson diagonalizable theorem
Let \(X\) be a smooth \(4\)-manifold. Suppose \(Q_{X}\) is definite that is the matrix \(Q_{X}\) is postive or negative definite, we have \(Q_{X} \cong \pm \begin{pmatrix} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \end{pmatrix} \).
Cf. Intersection forms.
One of the proofs is given by Seiberg-Witten invariant and following algebra result.
Let \(Q: \ZZ^{m} \otimes \ZZ^{m} \to \ZZ\) be a negative definite, unimodular form and let \(\Char(Q) = \{v \in \ZZ^{m} \mid Q(v, w) \equiv Q(w,w) \pmod 2\}\). Suppose that \(Q(v, v) + m \leq 0, \quad \forall v \in \Char(Q)\). Then \(Q \cong -I\).
Referenced: Geometric Topology, Characteristic class for 4-manifold.
TODO Dot notation
Elliptic fibration
A map \(q: X \to \Sigma\) is an elliptic fibration if there exists a finite set \(S \subset \Sigma\) such that \(X \backslash q^{-1}(S) \to \Sigma \backslash S\) is a fiber bundle whose fiber is a smooth curve of genus \(1\), that is the elliptic curve. We call \(q^{-1}(t)\) a regular fiber if \(t \not \in S\) and a singular fiber if \(t \in S\).
Cf. Vector bundle.
Exotic R^4
\(\RR^{4}\) has infinitely many smooth structures. While other Eucliean space has unique smooth structure by Stallings.
\(\RR^{4}\) has uncountably many smooth structures.
The construction follows from the oberservation for \(X = \CC P^{2} \shar 9 \overline{\CC P}^{2}\), we have \(Q_{X} \cong (-E_{8}) \oplus (-1) \oplus (1)\). Then if all \(\RR^{4}\) has same smooth structure, some kind of surgery gives impossible \(4\)-manifolds. By examing the construction carefully, one shows that there exists a parameter such that every two construction gives different smooth structures.
Exotic \(R^{4}\) can also be constructed using Knot theory.
TODO Exotic surfaces
TODO Fintushel-Stern knot surgery
The following theorem by Fintushel-Stern gives many exotic smooth structures.
Suppose \([T^{2}] \neq 0 \in H_{2}(X ; \RR)\), let \(X_{K}\) be the knot surgery along \(T^{2}\). Then \[SW_{X_{K}} = SW_{X} \cdot \Delta_{K}(e^{2[T]^{2}})\] where \(SW_{X} = \sum_{v \in \Char(X)} SW_{X}(v) e^{v}\) and \(\Delta\) is the Alexander polynomial
Given any smooth \(4\)-manifold \(X\) with
- \(b^{+}(X) \neq 0\), \(\pi_{1}(X) = 1\).
- \(SW_{X} \neq 0\).
- There exists \(T^{2} \to X\) embedding such that \([T^{2}] \neq 0\) and \(T^{2} \cdot T^{2} = 0\), \(\pi_{1}(X \backslash T^{2}) = 1\).
Then \(X\) has infinitely many smooth structure. In particular, all knonw symplectic \(4\)-manifold with \(b^{+} > 1\) satisfies this conditions.
Suppose \([T^{2}] \neq 0\) then \(X_{K} \cong X_{L}\) if and only if \(\pi_{1}(S^{3} \backslash K) \cong \pi_{1}(S^{3} \backslash L)\).
The conjecture is related to the open question, given \(K, L\) with \(\Delta_{K} = \Delta_{L}\) can \(X_{K} \not \cong_{diff} X_{L}\). Since there exists many knots with same Alexander polynomial, the question is important. However, we don’t have any tool to detect smooth structure other than Seiberg-Witten invariant.
Framed
See Framing.
Referenced: Jones-Markov trace.
Framing
Framing of a Link in \(\RR^{3}\) is an isotopy class of a continuous section of a normal bundle to \(L \subset \RR^{3}\).
Freedman’s classification of topological 4-manifold
- Let \(X_{0}, X_{1}\) be two simply connected topological \(4\)-manifolds. Then \(X_{0} \cong_{top} X_{1} \Leftrightarrow Q_{X_{0}} \cong Q_{X_{1}}, \ks(X_{0}) = \ks(X_{1})\).
- Given any unimodular, symmetric bilinear form \(Q\). Then
- Suppose \(Q\) is odd, i.e. there exists \(v\) such that \(Q(v,v)\) is odd, then any combination of \((Q, i)\) where \(i \in \{0,1\}\) can be realized as the intersection form and KS invariant of some simply connected topological \(4\)-manifold \(X\).
- Suppose \(Q\) is even, i.e. for every \(v\), \(Q(v,v)\) is even. Then \((Q, i)\) can be realized if and only if \(i \equiv \frac{\sigma(Q)}{8} \mod 2\).
Cf. Manifold, Kirby-Sieberman invariant, Whitehead theorem, Intersection forms, Signature.
By Freedman’s result, the Chern number \(c(X) = 2 \chi(X) + 3 \sigma(X)\), and Holomorphic Euler number \(\chi_{h}\) and \(t(X) = \begin{cases} 0 & Q_{X} \text{ is even.} \\ 1 & Q_{X} \text{ is odd.} \end{cases}\).
Referenced: Geometric Topology, Characteristic class for 4-manifold, Geography of 4-manifold.
Gabai’s lightbulb theorem
Given \(F \hookrightarrow X\), we say an embedded sphere \(\Sigma \hookrightarrow X\) is a geometric dual of \(F\) if \(\Sigma \cdot \Sigma = 0\) and \(F \pitchfork \Sigma = \{pt\}\). And \(F\) is \(\Sigma\)-essential if \(\pi_{1}(F \backslash \Sigma) \to \pi_{1}(X \backslash \Sigma)\) is trivial. The Gabai’s lightbulb theorem states
- Given any \(S^{2} \hookrightarrow S^{2} \times S^{2}\) with \(S^{2} \pitchfork (* \times S^{2}) = \{pt\}\). Then \(S^{2} \cong_{diff} S^{2} \times \{*\}\).
- Given any \(F_{1}, F_{2} \hookrightarrow X\) with \(\pi_{1}(X)\) no \(2\)-torsion. Suppose there exists a common geometric dual for \(F_{i}\) and \(F_{1}, F_{2}\) both \(\Sigma\)-essential. Then \(F_{1} \cong_{diff} F_{2}\).
Geography of 4-manifold
By Freedman’s classification of topological 4-manifold, the geography of \(4\)-manifold is the question which triple \((c, \chi_{h}, t)\) can be realized as smooth, Irreducible, simply connected \(X\).
The following conjecture relates the irreduciblity of \(4\)-manifold and Holomorphic Euler number.
For irreducible \(X\), \(\chi_{h}(X)\) or \(\chi_{h}(\bar{X})\) must be integer.
Also, we have following theorem.
\(\chi_{h}(X) \in \ZZ\) if and only if \(X\) has an almost complex structure.
For complex geography problem, we have inequalities for surface of general type, Bogomolov-Miyaoka-Yau inequality\(c \leq 9 \chi_{h}\) and Noether inequality \(c \geq 2 \chi_{h} - 6\). If \(X\) is minimal, simply conected then \(X \cong_{diff} \CC P^{2}\) or \(X \cong_{diff} S^{2} \times S^{2}\). If \(X\) is elliptic, then \(c = 0\). The currenst status of complex geography problem is in following diagram.
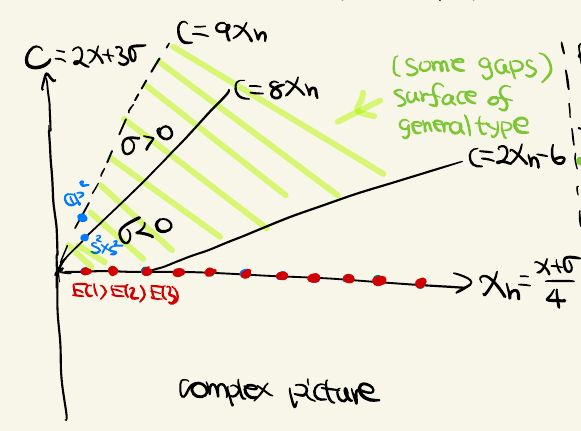
The current status of smooth geography problem is deduced from complex case by rational blow down.
However, the smooth simply connected case with \(c \geq 9 X_{h}\) or \(c < 0\) is completely unknown.
The current status of symplectic geography problem is in following picture.
The \(c < 0\) case is deleted by the theorem of Taubes.
If \(X\) is minimal symplectic with \(\pi_{1}(X) = 1\), then \(c \geq 0\).
There exists symplectic BMY conjecture.
Let \(X\) be a simply connected, symplectic \(4\)-manifold, then \(c(X) \leq 9 \chi_{h}(X)\).
Geometric braid
A geometric braid in \(\RR^{2} \times [0,1]\) is an embedding \(\hat{\beta} : [0,1]^{\coprod n} \to \RR^{2} \times [0,1]\) connecting \(\{x_{0}, \cdots, x_{n}\} \times \{0\}\) and \(\{x_{0}, \cdots, x_{n}\} \times \{1\}\) componentwise.
Referenced: Braid.
Geometric tangle
A geometric tangle is an embedding of \([0, 1]^{\coprod k} \coprod (S^{1})^{\coprod m}\) into \(\RR^{2} \times [0,1]\) such that images of endpoints of intervals are on \(\RR^{2} \times \{0\}\) and \(\RR^{2} \times \{1\}\), intersection of intervals is transversal to the planes and images of cirvles are strictly inside of \(\RR^{2} \times [0,1]\).
A based tangle is the regular isotopy class, preserving boundary points of a geometric tangle. And a standardized tangle is a based tangle with endpoints being in a line \(\RR \subset \RR^{2}\).
TODO Handle decomposition
Referenced: Monotone, Handle move, Morse complex, Morse theory.
Monotone
A Handle decomposition \(X_{0}| \cdots | X_{k}\) is called monotone if \(X_{i}\) only consists of \(i\)-handles for all \(i\).
Any manifold has a monotone handle decomposition.
Every manifold has a self-indexed Morse function.
Cf. Self-indexed Morse function.
Referenced: Handle move, Morse complex.
TODO Handle move
Any two Monotone Handle decomposition of \(X\) are related by the following handle moves
- handle slide
- creation / cancellation
h-Cobordism
With the same notation as in Corbordism, we say that \(W\) is h-cobordism if \(M_{0} \hookrightarrow W\) and \(M_{1} \hookrightarrow M\) are all homotopy equivalences.
The following theorem by Smale, Kirby-Siebenmann show that h-cobordism is powerful classification tool in high dimensional topology.
Let \(W\) be an h-cobordism (in \(\mathscr{C}\)) from \(M_{0}\) to \(M_{1}\). Suppose \(\pi_{1}(W) = 1\) and \(\dim(M_{0}) \geq 5\). Then \(W \cong_{\mathscr{C}} M_{0} \times [0,1]\).
The key lemma in the proof of the last theorem is by Whitney, which gives the mysterious dimension bound in the theorem.
Let \(F_{0}, F_{1}\) be connected, orientable manifolds smoothly embedded in \(M\). suppose
- \(\dim F_{0} + \dim F_{1} = \dim M \geq 5\).
- \(\pi_{1}(M) = \pi_{1}(M \backslash F_{0}) = \pi_{1}(M \backslash F_{1}) = 1\).
Then we can isotope \(F_{0}, F_{1}\) such that they intersect transversely at \(\abs{F_{0} \cdot F_{1}}\) points.
The key of the previous lemma is that all the intersection number gives positive or negative intersection sign. The transversity can be done in any dimension.
Referenced: Botany problem of 4-manifold, Poincarè conjecutre, Wall Theorem.
Hecke-Iwahori algebra
For Braid group \(B_{n}\), the elements \((s_{i} - q)(s_{i} + q^{-1})\) generates an ideal in the group algebra \(\CC[B_{n}]\). The Hecke-Iwahori algebra is the quotient algebra with respect to the ideal, i.e., \[H_{n}(q) = \langle s_{1}, \cdots, s_{n} \rangle\] such that \[s_{i}s_{i+1}s_{i} = s_{i + 1}s_{i}s_{i + 1},\; i = 1, \cdots, n - 1\] \[s_{i}s_{j} = s_{j}s_{i}, \; \abs{i - j} > 1\] \[(s_{i} - q)(s_{i} + q^{-1}) = 0\] The interesting case is that \(q\) be the root of \(1\).
\(H_{n}(q)\) is a deformation of \(\CC[S_{n}]\).
Heegaard diagram
A genus \(g\) Heegaard diagram is \((\Sigma_{g}, \alpha_{1}, \cdots, \alpha_{g}, \beta_{1}, \cdots, \beta_{g})\) consists of a genus \(g\) Orientable surface \(\Sigma_{g}\), two families of simple closed curves \(\alpha_{* }\), \(\beta_{* }\) such that \(\alpha_{i} \cap \alpha_{j} = \beta_{i} \cap \beta_{j} = 0 \) for \(i \neq j\) and \(\Sigma_{g} - \coprod \alpha_{i}, \Sigma_{g} - \coprod \beta_{i}\) are both connected.
Cf. Heegaard splitting.
Referenced: Trisection diagram.
Heegaard splitting
A genus \(g\) Heegaard splitting of \(3\)-manifold is a decomposition of \(Y\) into two genus \(g\) handle bodies.
Referenced: Heegaard diagram.
Hessian
The Hessian is the well-defined map \({\rm Hess} f_{p}: T_{p}X \otimes T_{p}X \to \RR\) defined by \(\left(\frac{\partial^{2}f}{\partial x_{i} \partial x_{j}}\right)\).
Referenced: Non-degenerate.
Holomorphic Euler number
We define the holomorphic Euler number by \(\chi_{h}(X) = \frac{\chi(X) + \sigma(X)}{4}\).
Referenced: Freedman’s classification of topological 4-manifold, Geography of 4-manifold.
HOMFLY invariant
Since Skein relations are compatible with Reidemeister moves, for every Link, we may consider its diagram \(D_{L}\) and we define \([D_{L}] = \langle L \rangle [O]\). Here \(O\) is one loop and \(\langle L \rangle \in \ZZ[A, B^{\pm 1}, C]\). \(\langle L \rangle\) depends only on \(L\) but not on representative diagram \(D_{L}\). \(\langle L \rangle\) is the HOMFLY invariant of framed links.
For unframed links, we also have HOMFLY invariants by consider \(L = L_{1} \coprod \cdots \coprod L_{n}\) as framed links and consider \(\langle \langle L \rangle \rangle = B^{- \sum_{i} w(L_{i})} \langle L \rangle\) where \(w(L_{i})\) is the winding number.
Homotopic slice
A Knot \(K \subset S^{3}\) is called homotopy slice if \(K\) bounds a smooth \(i:D^{2} \hookrightarrow X\) with \(\partial X = S^{3}\) such that \(i\) is homotopic to \(i': D^{2} \to \partial X\) relative to \(\partial D^{2} = K\).
Kronheimer and Mrowka has the following conjecture.
\(K\) is homotopy slice then the Rasmuusen invariant \(s(K) = 0\).
Cf. Rasmussen invariant.
The above conjecture is proved for \(X = \CC P^{2}\).
Index
See Non-degenerate.
Referenced: Morse inequality.
Integer homology 3-sphere
The integer homology 3-sphere is a \(3\)-manifold \(Y\) with \(H_{1}(Y; \ZZ) = 0\).
Freedman proved following result.
Any integer homology \(3\)-sphere bounds a contractible topological \(4\)-manifold.
Cf. Contractible.
Intersection forms
For \(4\)-manifold, we have nondegenerated bilinear form \[Q_{X}: H^{2}(X; \ZZ)/(tors) \times H^{2}(X; \ZZ)/(tors) \to \ZZ\] defined by \((\alpha \cup \beta)[X]\) called intersection form. It is a symmetric, unimodular form.
As an example of the intersection form, we have the intersection form of K3 surfaces \(Q_{X} = 2E_{8} \oplus 3 \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\)
Cf. K3 surfaces, E8.
We can generalized above intersection form to manifold with boundary. The interesection form is defined on \(V = \im(H_{2}(X) \to H_{2}(X, \partial X))/(torsion)\). \(Q_{X}(i_{* }(\alpha), i_{* }(\beta)) = (\pd(\alpha) \cap \pd(\beta)) \cdot [X]\).
For a manifold with boundary, the intersection form is still nondegenerate but not necessarily unimodular. In fact, we have the following proposition
Given any symmetric \(Q\) with \(\det(Q) \neq 0\), there exists a simply connected \(4\)-manifold \(X\) such that \(Q_{X} = Q\) and \(\abs{\det(Q)} = \abs{H_{1}(\partial X)}\).
Referenced: Lefschetz fixed point theorem, Donaldson diagonalizable theorem, Freedman’s classification of topological 4-manifold, Signature.
Irreducible
A simply connected, closed, oriented \(4\)-manifold \(X\) is irreducible if \(X \not \cong_{diff} X_{0} \shar X_{1}\) with \(X_{0}, X_{1} \not \cong S^{4}\).
Referenced: Geography of 4-manifold, Seiberg-Witten invariant.
Jones-Markov trace
There exists a Jones-Markov trace \(\tr: \tilde{B}_{n} \to k = \ZZ[q, q^{-1}][\frac{1}{(q - q^{-1})}]\) such that \[\tr(\beta \gamma \beta^{-1}) = \tr(\gamma)\] \[\tr(\beta s_{n}) = \tr(\beta t_{n}) = z \tr(\beta)\]
It defines invariants of Framed Links. To get a invariant of links, we consider Writhe number, \(\omega(\beta)\). We have \(\tr(\beta)z^{w(\beta)}\) is an invarinat of links.
For \(z = q^{2}\) the polynomial is the Jones polynomial.
TODO Jones polynomial
Referenced: Jones-Markov trace.
TODO Jones polynomial
Jones twist
A map \(\mu: V \to V\) is called Jones twist if \[(\mu \otimes \mu) R = R(\mu \otimes \mu)\] \[(\id \otimes \tr)(\id \otimes \mu) PR = z \id_{V}\]
TODO Khovanov homology
Referenced: Lee homology.
TODO Kirby calculus
TODO Kirby move
Kirby-Sieberman invariant
We define the set \({\rm Top}_{m} = \{\text{ homomorphism } f: \RR^{m} \to \RR^{m} \text{ such that } f(0) = 0\}\). And \({\rm PL}_{m} = \{\text{ piecewise linear homeomorphism} f: \RR^{m} \to \RR^{m} \text{ such that } f(0) = 0\}\).
The Kirby and Sieberman has following deep and mysterious theorem.
For \(m \geq 5\), \(k < m\). Then \(\pi_{k}({\rm Top}_{m}/ {\rm PL}_{m}) = \begin{cases} 0 & k \neq 3 \\ \ZZ/2 & k = 3 \end{cases}\).
So to have PL structure on \(X\), \(\dim X \geq 5\) we need to overcome the obstruction called Kirby-Sieberman invariant \(KS(X) \in H^{4}(X; \ZZ/2)\). So \(X\) has a PL-structure then \(\ks(X) = 0\). And for \(\dim X = 4\), \(\ks(X) = 0\) if and only \(X \times \RR\) has a PL-structure.
For \(\dim X \leq 7\), we have existence of piecewise linear structure equivalent to existence of smooth structure.
Referenced: Freedman’s classification of topological 4-manifold.
TODO Knizhnik–Zamolodchikov equation
Knot
A knot (in \(S^{3}\)) is an isotopy class of an Immersion \(\hat{K}: S^{1} \to S^{3}\), \(K = [\hat{K}]\).
Referenced: Positive, Link, Homotopic slice, Knots bounds algebraic surface, Linking number, Poincarè conjecutre, Unknot number.
Knots bounds algebraic surface
By Seiberg-Witten invariant, it is natural to ask when a Knot bounds an algebraic surface. The answer is the following theorem.
A knot \(K\) arises as \(K = S \pitchfork \partial D^{4}\) for some affine algebraic curve \(S \subset \CC^{2}\) if and only if \(K\) is quasi-positive. Moreover, suppose \(K = \bar{b}\), where \[b = \prod_{k = 1}^{m} w_{k} \sigma_{i_{k}} w^{-1}_{k}\] Then we can find \(S\) with \(g(S \cap D^{4}) = \frac{m - n + 1}{2}\), and therefore \(g_{S}(K) = \frac{m - n + 1}{2}\).
Cf. Quasi-positive, Slice genus.
For Positive knot, we have \(U_{K} = g_{S}(K)\) which is not true for quasi-positive knot.
TODO Lee homology
Cf. Khovanov homology.
Referenced: Rasmussen invariant.
Lefschetz hyperplane theorem
Let \(X\) be a hypersurface in \(\CC \PP^{n}\) defined by a single polynomial, then \(X \to \CC P^{n}\) induces isomorphism on \(\pi_{k}(-)\) if \(k < n - 1\).
The hypersurface in \(\CC P^{3}\) is simply connected.
Lickorish-Wallace theorem
Every closed orientable connected \(3\)-manifold can be obtained from a surgery on a link with coefficient \(\pm 1\).
Cf. Link, Orientation, Surgery.
Link
A link is an isotopy class of an Immersion \(\hat{L}: (S^{1})^{\times K} \to S^{3}\), \(L = \hat{L}\).
Cf. Knot.
Referenced: Diagram, Framing, HOMFLY invariant, Jones-Markov trace, Skein relations, Lickorish-Wallace theorem, Seifert surface.
Linking number
Let \(K_{1}, K_{2}\) be Oriented Knots in \(S^{3}\). We define the linking number \(lK(K_{1}, K_{2}) \in \ZZ\) by \[[K_{2}] = lK(K_{1}, K_{2})[m_{1}] \in H_{1}(S^{3} \backslash K_{1}) \cong \ZZ\] where \(m_{1}\) is the meridian of \(K_{1}\). The following is a sketch graph of meridian.

An alternative definition is consider \(\Sigma_{1}\) Seifert surface of \(K_{1}\) and then define \(lK(K_{1}, K_{2}) = \Sigma_{2} \cdot K_{1}\). Or we consider embeddings \(\Sigma_{1} \to D^{4}\), \(\Sigma_{2} \to D^{4}\) such that \(\partial \Sigma_{1} = K_{1}\), \(\partial \Sigma_{2} = K_{2}\) and define \(lK(K_{1}, K_{2}) = K_{1} \cdot K_{2}\).
TODO Mazur manifold
Milnor conjecture (theorem)
The Milnor conjecture is the following. (now a theorem)
For \(T_{p,q}\) the \((p,q)\)-torus knot, we have \[g_{S}(T_{p,q}) = \frac{(p - 1)(q - 1)}{2}\]
One can use local Thom conjecture (theorem) to prove.
Morse complex
Now we consider the complex constructed from Morse theory. We have \(X = X_{0} | X_{1} | \cdots | X_{n}\) Monotone. And for \(H_{k} \subset X_{k}\) and \(H_{k + 1} \subset X_{k + 1}\), we define the pairing \(\langle H_{k}, H_{k + 1}\rangle\) the intersection number of the belt sphere of \(H_{k}\) and attaching sphere of \(H_{k + 1}\). Then we have Morse complex \(C_{k}^{n}(X) = \ZZ \langle H_{k}^{1}, \cdots, H_{k}^{a_{k}}\rangle\) and define the differential to be \[\dif H_{k}^{i} = \sum_{j} \langle H_{k - 1}^{j}, H_{k}^{i}\rangle H_{k - 1}^{j}\] We have that \(\dif^{2} = 0\).
Cf. Handle decomposition.
Referenced: Morse inequality.
Morse function
A Morse function is a funciton if all critical points are non-degenerate. If the origin manifold \(X\) has boundary, then \(f^{-1}(\max f) = \partial X\).
Referenced: Monotone, Self-indexed.
Self-indexed
A Morse function is called self-indexed if for all \(x \in {\rm crit}(f)\), we have \(f(x) = {\rm index}(x)\).
Referenced: Monotone.
Morse inequality
From Morse complex, we have that
For any \(0 \leq k \leq \dim(X)\), we have that \[\sum_{0 \leq i \leq k}(-1)^{k - i}b_{i}(X) \leq \sum_{0 \leq i \leq k} (-1)^{k - i} \abs{{\rm crit}_{i}(f)}\]
Suppose all critical points of \(f\) have even indices, then \(b_{2k}(X) = \abs{{\rm crit}_{2k}(f)}\).
Cf. Critical point, Index.
Morse theory
Let \(f\) be a smooth real valued function on manifold M. Let \(a < b\) and suppose that the set \(f^{-1}[a,b]\) is compact and contain no critical points of \(f\). Then \(M^{a}\) is diffeomorphic to \(M^{b}\). Furthermore, \(M^{a}\) is a deformation retract of \(M^{b}\), inclusion map \(M^{a} \to M^{b}\) is a homotopy equivalence.
The theorem supplies the condition when the retraction is possible.
If \(f\) is a differentiable function on a manifold \(M\), with no degenerate critical points, and if each \(M^{a}\) is compact, then \(M\) has the homotopy type of a CW-complex, with one cell of dimension \(\lambda\) for each critical point of index \(\lambda\).
Let \(\phi_{0}\) and \(\phi_{1}\) be homotopic maps from the sphere \(\dot{e^{\lambda}}\) to \(X\). Then the identity map of \(X\) extends to a homotopy equivalence \(k:X \cup_{\phi_{0}} e^{\lambda} \to X \cap_{\phi_{1}} e^{\lambda}\).
\begin{align} k(x) = x && x \in X \\ k(tu) = 2tu && 0 \leq t \leq 1/2 \\ k(tu) = \phi_{2-2t}(u) && 1/2 \leq t \leq 1 \end{align}
Let \(\phi:\dot{e^{\lambda}} \to X\) be an attaching map. Any homotopy equivalence \(f:X \to Y\) extends to a homotopy equivalence \(F:X \cup_{\phi}e^{\lambda} \to Y \cup_{f\phi}e^{\lambda}\)
Given a Morse function, we have a Handle decomposition.
Suppose \(f^{-1}( r) \cap {\rm crit}(f) = \{x_{1}, \cdots, x_{l}\}\). Let \(a_{i} = {\rm index}(x_{i})\). Then for \(\epsilon > 0\) small enough, we have \[X_{\leq r + \epsilon} = X_{\leq r - \epsilon} \cup (H_{a_{1}} \coprod H_{a_{2}}) \cdots \coprod H_{a_{l}}\] where \(H_{i}\) is the \(i\)-handle.
Poincarè conjecutre
We have following generalized Poincarè conjecture which is proved by various people in various dimensions.
Let \(M\) be a \(n\)-dimensional topological manifold homootpy equivalent to \(S^{n}\). Then \(M \cong_{top} S^{n}\).
For \(n \geq 6\), we can give a proof by h-Cobordism.
However, the smooth structure on \(S^{n}\) may not be unique. \(S^{2k + 1}\) has unique smooth structure if and only if \(2k + 1 = 1,3,5,61\).
The dimension \(4\) smooth Poincaré conjecture is still open. A possible approach is suggested by Freedman-Gompf-Morrison-Walker using Knot on \(S^{4}\) to do some surgery and making contradiction.
TODO Rasmussen invariant
Cf. Lee homology.
Referenced: Homotopic slice, Slice genus.
TODO Rational blow down
Realization of Finite Presnetation Group as Fundamental Group of Manifolds
We have following theorem by Markov, showing that any finite presentation group can be realized as a fundamental group of a manifold.
Given any presentation of a group \(G = \langle g_{1}, \cdots, g_{m} \mid r_{1}, \cdots, r_{m}\rangle\), one can construct a \(n\)-dim \(n \geq 4\) manifold \(M\) with \(\pi_{1}(M) = G\).
Together with the following theorem of Adyan-Rubin, we show that a complete classification of high dimensional manifold is impossible.
There does not exist an algorithm that tells whether a given presentation yields the trivial group.
Regular value
See Critical value.
Representation of braids
The following proposition relates the representation of Braid group to Yang-Baxter equation.
If \(R\) satisfies the Yang-Baxter equation, the mapping \[\rho: B_{n} \to \aut(V^{\otimes n})\] \[\rho(s_{i}) = 1 \otimes \cdots \otimes PR \otimes \cdots \otimes 1\] where \(P(x \otimes y) = y \otimes 1\) extends uniquely to a representation of \(B_{n}\) in \(V^{\otimes n}\).
Rokhlin Theorem
Let \(X\) be a smooth spin \(4\)-Manifold. Then \(16 | \sigma(X)\).
Cf. Signature.
Referenced: Geometric Topology.
Seiberg-Witten equation
The Seiberg-Witten equation is the following equations for \((A, \phi \in \Gamma^{S^{+}})\) \[ \begin{cases} F_{A^{\tau}}^{+} - \rho^{-1}(\phi^{*} \phi)_{0} = 0 & \\ \dirac_{A}^{+} \phi = 0 & \end{cases} \] Here \((\phi^{* } \phi)_{0}: \psi \to \langle \psi, \phi> \cdot \phi - \frac{\abs{\phi}^{2}}{2} \psi\). We have \(((\phi^{* } \phi)_{0})^{* } = (\phi^{* } \phi)_{0}\) and \(\tr (\phi^{* } \phi)_{0} = 0\).
Referenced: Seiberg-Witten moduli space.
Seiberg-Witten invariant
For simply connected \(4\)-manifold \(X\), we have a natural \(S^{1}\) bundle \(P\) on Seiberg-Witten moduli space \(\mathscr{M}_{SW}\) coming from the Coulomb guage description. So we define the Seiberg-Witten invariant by \[SW(X, S) = c_{1}(P)^{d(S)/2} \cdot [\mathscr{M}_{SW}] \in \ZZ\] where \(d(S)\) is the dimension of the Seiberg-Witten moduli space. When \(d(S)\) is odd, we simply define the Seiberg-Witten invariant to be \(0\).
We have following conjecture for Seiberg-Witten invariants called simple type conjecture
If \(d(S) > 0\), \(b^{+ } > 1\), then \(SW(X, S) = 0\).
The symplectic case is proved by Taubes.
The simple type conjecture holds for symplectic manifolds.
Let \(\Char(X)\) denote the set \(\{K \in H^{2}(X; \ZZ) \mid K \cdot [\Sigma] = \Sigma \cdot \Sigma \pmod 2\}\), and we define the \(SW\) as a map \[SW(\alpha) = \sum_{S \in \Spin^{\CC}(X), c_{1}(S) = K} SW(X, S)\] The Seilberg-Witten invariants have following properties:
- \(SW_{X}(K) = 0\) for all but finitely many \(K \in \text{char}(X)\). Those \(K\) are called basic classes.
- If \(X\) has postive scalar curvature, then \(SW_{X}(K) = 0\) for every \(K\).
- \(SW_{X}(-K) = (-1)^{b_{2}^{+}(X) - b_{1}(X) + 1} SW_{X}(K)\).
- If \(X \cong_{diff} X_{1} \shar X_{2}\) with \(b_{2}^{+}(X_{1}), b_{2}^{+}(X_{2}) > 0\), then \(SW_{X}(K) = 0\) for every \(K\).
- Blow-up formula: If \(X \cong_{diff} X' \shar \overline{\CC P}^{2}\), then basic classes of \(X\) are \(\{K \pm \pd E \mid K \text{ is a basic class of } X'\}\). Moreover, \(SW_{X}(K \pm \pd E) = SW_{X'}(K)\).
- If \(X\) is an algebraic surface, then \(SW_{X}(c_{1}(TX)) = \pm 1\). (Witten)
- If \(X\) is symplectic, and \(J\) compatible almost complex structure, then \(SW_{X}(c_{1}(TX, J)) = \pm 1\). (Taubes)
- Adjunction inequality. (See below)
As an application of Taubes result on symplectic \(4\)-manifold, we consider the following corollary.
If \(X\) is symplectic, and \(X \cong_{diff} X_{1} \shar X_{2}\). Then \(b_{2}^{+}(X_{1})\) or \(b_{2}^{+}(X_{2})\) must be \(0\).
Some more works show the following theorem by Kotschick, Taubes.
Let \(X\) be a simply connected, symplectic \(4\)-manifold. Then \(X\) is minimal if and only if \(X\) is irreducible.
Cf. Irreducible.
We state the adjunction inequality by Kronheimer-Mrowka, Ozsrath-Szabo, Fintushel-Stern.
Let \(\Sigma \to X\) be a smoothly embedded essential surface (\([\Sigma] \neq 0\)), where \(b^{+}_{2}(X) > 1\) and \(S \in \Spin^{\CC}(X)\) such that \(SW_{X}(S) \neq 0\). Then we have
- If \(\Sigma \cdot \Sigma \geq 0\), then \[2g(\Sigma) - 2 \geq \Sigma \cdot \Sigma + \abs{c_{1}(S) \cdot [\Sigma]}\]
- Assume \(X\) is simple type, then same results holds even if \(\Sigma \cdot \Sigma < 0\).
Since the symplectic \(4\)-manifold is simple type, so we can deduce the following symplectic Thom conjecture.
Let \((X, \omega)\) be a symplectic \(4\)-manifold. Let \(\Sigma \stackrel{i}{\hookrightarrow} X\) be a symplectic surface, that is \(i^{*}(\omega)\) is nowhere vanishing on \(\Sigma\). Then \(\Sigma\) is genus minimizing in its homology class.
To apply the above theorem, we have a priori known a symplectic surface. Because not all homology class can be represented by a simplectic surface. There are two major obstructions: first, the symplectic area; second, the adjunction formula in Seiberg-Witten theory. However, you can always find immersed symplectic surface representing a homology class if the symplectic area is positive; and if \(\dim X \geq 6\), then you can make the surface embedded. Again, \(4\) is the critical dimension.
Referenced: Geometric Topology, Donaldson diagonalizable theorem, Fintushel-Stern knot surgery, Knots bounds algebraic surface, Thom conjecture (theorem).
Seiberg-Witten moduli space
By Seiberg-Witten equation, the solution forms Seiberg-Witten moduli space, \[\mathscr{M}_{SW} = \{\text{Seiberg-Witten solutions}\}/ \mathscr{G}\] where \(\mathscr{G} = \Gamma(X, \End(S^{+}, \rho)) = C^{\infty}(X, U(1))\) acts on \(\{(A, \phi)\}\) by \(u \cdot (A, \phi) = (A - u^{-1} \dif u, u \cdot \phi)\).
Or we can formulate in another way by fixed the Coulomb gauge with respect ot a base Spin^C connection \(A_{0}\) by setting \(\dif^{* }(A - A_{0}) = 0\). \[\mathscr{M}_{SW} = \{\text{Coulomb gauge Seiberg-Witten solutions}\}/ \mathscr{G}_{h}\] where \(\mathscr{G}_{h} = \{\text{harmonic map }X \to S^{1}\} \cong H^{1}(X; \ZZ) \times S^{1}\).
The following result is important and magic by Clifford Taubes.
\(\mathscr{M}_{SW}\) is compact.
The proof relies on the estimate of the \(\abs{\phi}\) and elliptic boosting technique for elliptic partial differential equations.
However, in general the moduli space is not a manifold, but in \(b^{+ }_{2} > 0\) case, by perturbing the equation a little, we can get an Oriented manifold of dimension \(\frac{c_{1}(S)^{2} - \sigma(X)}{4} + b^{1}(X) - b_{2}^{+}(X)\). The result depend on Sard-Smale theorem which is an analog of Sard theorem in infinite dimensional case. For \(b^{ +} > 1\), all such moduli space is equivalent, but in \(b_{2}^{ +} = 1\) case, we have \(2\) choices.
Referenced: Seiberg-Witten invariant.
Seifert genus
See Seifert surface.
Referenced: Thom conjecture (theorem).
Seifert surface
For any Oriented Link \(L \to S^{3}\), there exists an embedded orientable surface \(\Sigma \to S^{3}\) with \(\partial \Sigma = L\). Such surface is called Seifert surface.
The Seifert genus \(g(K)\) is the minimal genus of Seifert surface. The slice genus \(g_{S}(K)\) is the minimal genus of orientable \(\Sigma \to D^{4}\) with \(\partial \Sigma = K\).
Obviously, we have \(g_{S}(K) \leq g(K)\).
Referenced: Linking number, Seifert genus, Slice genus.
Self-dual
A \(n\)-form \(w\) on \(2n\) manifold is called self-dual if \(* w = w\).
Any \(n\)-form can be decomposed to a sum of self-dual part and Anti-self-dual part.
Referenced: Anti-self-dual, Dirac operator.
Signature
For Intersection forms \(Q_{X}\), we have \(b^{+ }(X)/b^{- }(X)\) denote the number of the positive and negative eigenvalues of \(Q_{X}\). And we define the signature to be \(\sigma(X) = b^{+ }(X) - b_{2}^{-}(X)\).
Referenced: Characteristic class for 4-manifold, Freedman’s classification of topological 4-manifold, Rokhlin Theorem.
Skein relations
We now consider a vector space \(V\) of formal \(\ZZ\) linear combinations of Diagrams of Links modulo Reidemeister moves. The Skein relations are defined by
 where \(A, B, C\) are formal variables and \(B\) is invertible. We have
\[C = \frac{B - B^{-1}}{A}\]
where \(A, B, C\) are formal variables and \(B\) is invertible. We have
\[C = \frac{B - B^{-1}}{A}\]
Also, we Skein is related to Reidemeister moves.
Skein relations are compatible with Reidemeister moves.
Referenced: HOMFLY invariant.
Slice genus
See Seifert surface.
The slice genus is bounded below by Rasmussen invariant.
Referenced: Clasp number, Knots bounds algebraic surface, Slice ribbon conjecture.
Slice ribbon conjecture
We say a knot \(K\) is slice if \(g_{S}(K) = 0\) (Slice genus). And say \(K\) is ribbon if \(K\) bounds immersed \(D^{2} \subset S^{3}\) such that self intersection of \(D^{2} = \coprod \text{arcs}\). We know that ribbon is a slice, the conjecture is the converse also holds.
Any slice knot is ribbon.
Smale conjecture
The Smale conjecture for dimension \(n\) means
The map \(O(n + 1) \to {\rm Diff}(S^{n})\) is homotopy equivalence.
The conjecture is true for \(n \leq 3\) and false for \(n \geq 4\). The last case \(n = 4\) was proved in around 2018.
Spin^C connection
A unitary connection \(A\) on \(S\) is spin\(^{\CC}\) connection if \[\nabla_{A}(\rho(v) \cdot s) = \rho(v) \cdot \nabla_{A} s + \rho(\nabla_{LC} v) \cdot s\] for every \(v \in \Gamma(T_{* }X), s \in \Gamma(s)\). Here \(\nabla_{LC}\) is the Levi-Civita connection which relies on Riemannian metric.
Referenced: Dirac operator, Seiberg-Witten moduli space.
Spin^C structure
A Spin\(^{\CC}\) structure on \(X\) is a Hermitian bundle \(S \to X\) with bundle map \(\rho: T_{* }X \to \End(S)\) such that for all \(x\), \(\rho_{x}: T_{x}X \to \End(S_{x})\) is an irreducible Clifford module. Consider \(\pi = \rho(e_{1} \cdots e_{n})\), we have \(\pi^{2} = -1\). So \(S = S^{+} \oplus S^{-}\) by \(\pi\) action.
Spin\(^{\CC}\) structure is useful in \(4\)-manifold by following theorem.
Any \(4\)-manifold has a spin\(^{\CC}\) structure.
which result from the following proposition
A \(n\)-dimensional manifold \(X\) has a spin\(^{\CC}\) structure if and only if \(w_{2}(TX) \in \im(H^{2}(X; \ZZ) \to H^{2}(X; \ZZ/2))\).
Spin structure
Let \(\SO(n) \to {\rm Fr} \to X\) be the frame bundle of a smooth Manifold. A spin structure is a lift of \({\rm Fr}\) to a \(\Spin(n)\) bundle.
We have following lemma on the existence of spin structure.
\(X\) has a spin strucutre if and only if the second Stiefel-Whitney class \(\omega_{2}(X) = 0\). Furthermore, when \(\dim X = 4\) and \(\pi_{1} = 1\), \(X\) has a spin structure if and only if \(Q_{X}\) is even.
TODO Surgery
Referenced: Lickorish-Wallace theorem.
Tangle
A tangle is the regular isotopy class of a standardized Tangle with respect to deformation of endpoints.
Referenced: Tangle.
Thom conjecture (theorem)
The Thom conjecture is the following, now a theorem.
For \(X = \CC P^{2}\) and \(d > 0\), we have \[\min \{g(\Sigma) \mid \Sigma \hookrightarrow X, [\Sigma] = d \pd (\CC P^{1})\} = \frac{(d - 1)(d - 2)}{2}\]
Cf. Seiberg-Witten invariant, Seifert genus.
The following corolloary called local Thom conjecture is useful.
Let \(\Sigma \hookrightarrow \CC^{2}\) be an affine, smooth algebraic curve. Then \(\Sigma\) is locally genus miminizing, that is, for all \(D^{4} \in \CC^{2}, S \hookrightarrow D^{4}\) such that \(\partial D^{4} \pitchfork \Sigma = K\) and \(\partial S = K\), we have \(g(S) \geq g(\Sigma \cap D^{4})\).
Referenced: Milnor conjecture (theorem).
Trisection
Let \(X\) be a closed smooth Oriented connected \(4\)-manifold. For \(0 \leq k \leq g\), a \((g, K)\)- trisection of \(X\) is a decomposition \(X = X_{1} \cap X_{2} \cap X_{3}\) such that
- \(X_{i} \cong_{diff} \shar^{k}(S^{1} \times B^{3})\)
- \((X_{i} \cap X_{j}) = H_{ij} \cong_{diff} \shar^{g}(S^{1} \times B^{2})\)
- \(X_{1} \cap X_{2} \cap X_{3} = \Sigma_{g}\)
The following theorem of Gay and Kirby shows that trisection exists for any Orientable \(4\)-manifold and unique in some sense.
- Every closed smooth connected oriented \(4\)-manifold admits a trisection.
- Any two trisection diagrams of \(X^{4}\) are related by a sequence of particular moves.
Trisection diagram
A trisection diagram is a set of three curves \(\{\alpha_{i}\}, \{\beta_{i}\}, \{\gamma_{i}\}\) on \(\Sigma_{g}\) with \(1 \leq i \leq g\) such that any two collection is a Heegaard diagram for \(\shar^{k}(S^{1} \times S^{2})\).
Unknot number
Given a Knot \(K\), we define the unknotting number \(U(K)\) the minimal number that a knot Diagram of \(K\) can be made into an unknot.
Referenced: Clasp number.
Wall Theorem
Let \(M_{0}, M_{1}\) be simply-connected smooth \(4\)-manifold. Suppose \(M_{0} \cong_{homotopy} M_{1}\). Then
- \(M_{0}\) is smoothly h-cobordant to \(M_{1}\).
- For \(m \geq 0\), \(M_{0} \shar^{m} (S^{2} \times S^{2}) \cong_{diff} M_{1} \shar^{m} (S^{2} \times S^{2})\).
All known example show that \(m = 1\) is already enough but the proves requires large enough \(m\). Is the theorem not strong enough, or our understanding of 4-manifold too shallow?
The theorem also shows that h-Cobordism theorem fails for \(n = 4\).
Whitehead theorem
The Whitehead theorem is of the following form:
Suppose \(\pi_{1}(X_{1}) = \pi_{1}(X_{2}) = 1\). Then \[Q_{X_{0}} \cong Q_{X_{1}} \Rightarrow X_{0} \cong_{homotopy} X_{1}\]
The proof relies on the following lemma of Hopf.
\[\pi_{3}(S^{2} \vee \cdots \vee S^{2}) \cong \{n \times n \text{ symmetric matrices with integer coefficient}\}\] The left hand side has \(n\) copies of \(S^{2}\) and the isomorphism is group homomorphism.
Referenced: Freedman’s classification of topological 4-manifold.
Writhe number
We define the Writhe number of \(\beta\) to be

Referenced: Jones-Markov trace.
Yang-Baxter equation
A morphism \(R: V \otimes V \to V \otimes V\) satisfies the Yang-Baxter equation if \[R_{12}R_{13}R_{23} = R_{23}R_{13}R_{12} \in \End(V^{\otimes 3})\] where \(R_{12} = R \otimes 1\) and so on.
An solution is given by \[R(e_{i} \otimes e_{j}) = \begin{cases} q e_{i} \otimes e_{i} & i = j \\ e_{i} \otimes e_{j} & i < j \\ e_{i} \otimes e_{j} + (q - q^{-1})e_{j} \otimes e_{i} & i > j \end{cases} \]
Referenced: Representation of braids.
Quantum Fields and Strings
TODO Cobordism conjecture
TODO Extended topological quantum field theory
Super algebra
A super algebra over \(k\) is a Super vector space \(A\), with a given morphism \(A \otimes A \to A\). \(A\) is associative if \((xy)z = x(yz)\). A unit is an even element \(1\) such that \(1 x = x 1 = x\). \(A\) is commutative if \[xy = (-1)^{p(x)p(y)}yx\] for homogeneous elements.
We can define the module for algebra \(A\). And we make left module right module by \[m \cdot a := (-1)^{p(m)p(a)} a \cdot m\]
We also have opposite algebra \(A^{o}\) of \(A\) by product \[x \cdot_{opp} y = (-1)^{p(x)p(y)}y \cdot x\]
We can define the tensor product of modules and algebras naturely.
Super vector space
A super vector space is a \(\ZZ/2 \ZZ\) graded vector space \[V = V_{0} \oplus V_{1}\] An element \(v\) of \(V_{0}\) (resp. \(V_{1}\)) is said to be even (resp. odd). Its parity in \(\ZZ / 2 \ZZ\) is denoted \(p(a)\). And morphism between super vector spaces is degree presevering linear map.
We have parity reversing functor \(\Pi\) such that \((\Pi V)_{0} = V_{1}\) and \((\Pi V)_{1} = V_{0}\). Also we use the notation \(m_{0} \mid m_{1}\) to denote the dimension of \(V\) with \(\dim V_{0} = m_{0}\) and \(\dim V_{1} = m_{1}\).
The tensor product is defined by \((V \otimes W)_{k} = \oplus_{i + j = k} V_{i} \otimes W_{j}\). We define the commutativity isomorphism \[c_{V,W}: V \otimes W \to W \otimes V, v \otimes w \to (-1)^{p(v)p(w)} w \otimes v\] By above definition, we have the following diagram commutes.
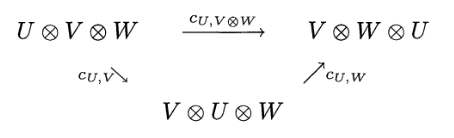
Referenced: Super algebra.
TODO Topological quantum field theory
Chern-Weil theory
See Chern class.
Chern-Simons functional
For \(A\) a connection on \(SU(2)\) principal bundle on manifold \(M\). We usually denote \[CS(A) = \frac{1}{8 \pi^{2}}\int_{M} \tr(F_{A} \wedge F_{A}) \in \RR/\ZZ\] called Chern-Simons functional, where \(F_{A}\) is the Curvature.
Or on 3-manifold, we define for Connection \(A\) (matrix valued 1 form), \[CS(A) = \frac{1}{8 \pi^{2}} \int_{Y} \tr(A \wedge \dif A + \frac{2}{3}A \wedge A \wedge A) \in \RR/\ZZ\]
Critical poiont of Chern-Simons functional are Flat connections and corresponds to group homomorphism \(\rho: \pi_{1}(M) \to SU(2)\).
Yang-Mills equation
Let \(P\) be a \(SU(2)\) bundle over \(4\)-manifold \(M\), then we call \[F_{A}^{+} = 0\] Anti-self-dual equation. The connection satisfying the equation minimizing energy equaiton Yang-Mills functional \[YM(A) = \int_{M} \abs{F_{A}}^{2}\] Critical point of Yang-Mills functional is given by Yang-Mills equation
\begin{equation*} \begin{cases} d^{*}_{A}F_{A} = 0 & \\ d_{A} F_{A} = 0 & \end{cases} \end{equation*}
The second equation is Bianchi identity (Cf. Curvature) and is automatically satisfied. In fact, solutions of anti-self-dual equation is a special solutions of the Yang-Mills equation, because it takes globally minimal value.
Algebraic Number Theory
Apart from algebraic number theory, the theory of cohomology of groups is also put here. The main reference is [milne2020a] and [kedlaya2021], for detailed proof see these and references there.
Abstract class field theory
If \(L/K\) is a cyclic extension of local fields, then we have \(\shar H_{T}^{0}(\Gal(L/K), L^{*}) = [L : K], \shar H_{T}_{-1}(\Gal(L/K), L^{*}) = 1\). We can construct the reciprocity map from above two equality. Such theory is called abstract class field theory.
Adèle
Let \(K\) be a number field of degree \(n\). It then has \(n\) distinct embeddings \(\tau: K \to \CC\). The product embedding \[j: K \to \prod_{\tau} \CC, a \to (\tau(a))_{tau}\] induces an isomorphism of \(K_{\CC} = K \otimes_{\QQ} \CC\), which induces Hermitian inner product. By considering the involution by complex conjugation, then we have \(K_{\RR}\). We have embedding \(K\) into \(K_{\RR}\), \(\mathfrak{o}_{K}\) corresponds to a lattice in \(K_{\RR}\).
For \(K\) a number field, there is a natural isomorphism of compact topological rings \[\hat{\mathfrak{o}_{K}} \to \prod_{\mathfrak{p}} \varinjlim_{m} \mathfrak{o}_{K} / \mathfrak{p}^{m}\] where \(\mathfrak{p}\) runs over prime ideals of \(\mathfrak{o}_{K}\).
We define the ring of finite adèles \(\mathbb{A}_{\QQ}^{fin}\) as any of the following isomorphic objects:
- the tensor product \(\hat{\ZZ} \otimes_{\ZZ} \QQ\).
- the direct limit of \(\frac{1}{n} \hat{\ZZ}\) over all nonzero integers \(n\).
- The Restricted topological product \(\prod_{p}' \QQ_{p}\), where we only allow tuples \((\alpha_{p})\) for which \(\alpha_{p} \in \ZZ_{p}\) for almost all \(p\).
We define the ring of adèles over \(\QQ\) as \(\mathbb{A}_{\QQ} = \RR \times \mathbb{A}_{\QQ}^{fin}\). Then \(\mathbb{A}_{\QQ}\) is a locally compact topological ring with a canonical embedding \(\QQ \to \mathbb{A}_{\QQ}\). We refer to the elements of \(\QQ\) as principal adèles with \(\mathbb{A}_{\QQ}\).
\(\QQ\) is discrete in \(\mathbb{A}_{\QQ}\).
for general number field \(K\). We define the ring of finite adèles \(\mathbb{A}_{K}^{fin}\) as following isomorphic objects:
- the tensor product \(\hat{\mathfrak{o}_{K}} \otimes_{\mathfrak{o}_{K}} K\);
- the direct limit of \(\frac{1}{\alpha} \hat{\mathfrak{o}_{K}}\) over all nonzero \(\alpha \in \mathfrak{o}_{K}\);
- the restricted direct product of the pairs \((K_{\mathfrak{p}}, \mathfrak{o}_{K_{\mathfrak{p}}}\) over all primes \(\mathfrak{p}\) of \(K\).
The ring of adèles is \(K_{\RR} \times \mathfrak{A}_{K}^{fin}\).
We have \[\abs{x}_{K} = \prod_{v} \abs{x}_{v}\] where if \(v\) is real take real absolute value, \(v\) complex, square of the absolute value and \(v\) finite Place normalized so that \(\abs{p}_{v} = p^{-1}\).
If \(\alpha \in K\), then \(\abs{\alpha}_{K} = 1\).
The subset \(K\) of \(\mathbb{A}_{K}\) is discrete.
The quotient group \(\mathbb{A}_{K}/K\) is compact.
Adelic reciprocity law
The adelic reprocity law is the following
There is a canonical map \(r_{K}: C_{K} \to \Gal(K^{ab}/K)\) which induces, for each Galois extension \(L/K\) of number fields, an isomorphism \(r_{L/K}: C_{K}/ \nm_{L/K} C_{L} \to \Gal(L/K)^{ab}\). Moreover, \(\nm_{L/K} C_{L}\) is an open subgroup of \(C_{K}\).
We have similar existence theorem and norm limitation theorem
For every number field \(K\) and every open subgroup \(H\) of \(C_{K}\) of finite index, there exists a finite extension \(L\) of \(K\) such that \(H = \nm_{L/K} C_{L}\).
Let \(L/K\) be an extension of number fields and put \(M = L \cap K^{ab}\). Then \(\nm_{L/K}C_{L} = \nm_{M/K} C_{M}\).
The following local-global compatibility is important to global class field theory. We define a map \(r_{K,v}:K_{v}^{*} \to G_{v} \subset G\) as local reprocity map if \(v\) is finite place, sign map if \(v\) is real place, trivial map if \(v\) is complex place. Then we define \[\tilde{r}_{K}: I_{K} \to G, (\alpha_{v}) \to \prod_{v} r_{K,v}(\alpha_{v})\]
For \(L/K\) an abelian extension of number fields, the map \(\tilde{r}_{K}: I_{K} \to \Gal(L/K)\) is trivial on \(K^{*}\) an factor through map \(C_{K} \to \Gal(L/K)\). And \(C_{K}/U \to \Gal(L/K)\) is the required Artin map.
Approximation theorem
The following theorem is referred to as approximation theorem.
Let \(S\) be a finite set of places of \(K\). For each \(v \in S\), let \(U_{v}\) be an open subgroup of \(K_{v}\). Then \(K \cap \cap_{v \in S} U_{v} \neq 0\).
Artin’s reciprocity law
Let \(L/K\) be a finite abelian extension of number fields. For each prime \(\mathfrak{p}\) of \(K\) that does not Ramify in \(L\), let \(\mathfrak{q}\) be a prime of \(L\) over \(K\), and put \(\kappa = \mathfrak{o}_{K} / \mathfrak{p}\) and \(\lambda = \mathfrak{o}_{L}/ \mathfrak{q}\). Then the residue field extension \(\lambda/ \kappa\) is an extension of finite fields, so it has a canonical generator \(\sigma\), the Frobenius element, which acts by rasing to \(q\)-th power. Since \(\mathfrak{p}\) does not ramify, the decomposition group \(G_{\mathfrak{q}}\) is isomorphic to \(\Gal(\lambda/ \kappa)\), so we get a canonical element of \(G_{\mathfrak{q}}\). We say it to be Frobenius of \(\mathfrak{p}\) since in abelian Galois group the conjugaton has no effect.
Now for \(\mathfrak{m}\) divisible by all primes of \(K\) which ramify in \(L\), define the homomorphism called Artin map \[J^{\mathfrak{m}}_{K} \to \Gal(L/K), \; \mathfrak{p} \to {\rm Frob}_{\mathfrak{p}}\]
The Artin’s reciprocity law is the following theorem
There exists a formal product \(\mathfrak{m}\) of places of \(K\), including all places over which \(L\) ramifies, such that \(P^{\mathfrak{m}}_{K}\) belongs to the kernel of the Artin map.
Augmentation ideal
Let \(M_{G}\) denote the maximal quotient of \(M\) on which \(G\) acts trivially. Then we have \(M_{G} = M / M I_{G}\), where \(I_{G}\) is the augmentation ideal of \(\ZZ[G]\) \[I_{G} = \{ \sum_{g \in G} z_{g} [g] \mid \sum_{g} z_{g} = 0\}\] We call \(M_{G}\) the group of \(G\)-coinvariants. \(M \to M_{G}\) is right exact but not left exact.
Brauer group
For any field \(K\), the group \(H^{2}(\Gal(\bar{K}/K), \bar{K}^{*})\) is called the Brauer group of \(K\), denoted by \({\rm Br}(K)\).
We have following isomorphism
\[H^{2}(K_{nr}/K) = Br(K) = \QQ / \ZZ\]
The left hand side means \(H^{2}(\Gal(K^{ur}/K), (K^{ur})*)\).
The valuation map \(v: K_{nr}^{*} \to \ZZ\) defines an isomorphism \(H^{2}(K_{nr}/ K) \to H^{2}(\hat{\ZZ}, \ZZ)\).
We consider the map \({\rm inv}\) we have isomorphism \[H^{2}(K_{nr}/K) \xrightarrow{v} H^{2}(\hat{\ZZ}, \ZZ) \xrightarrow{\delta^{-1}} \Hom(\hat{\ZZ}, \QQ/\ZZ) \xrightarrow{\gamma} \QQ/\ZZ\]
Let \(L/K\) be a finite extension of degree \(n\). Then \[{\rm inv}_{L} \circ {\rm Res}_{K/L} = n . {\rm inv}_{K}\]
Referenced: Brauer group.
Chebotarëv density theorem
The Caebotarëv density theorem is the following.
Let \(L/K\) be a Galois extension of number fields with Galois group \(G\). Then for any \(g \in G\) there exist infinity many primes \(\mathfrak{p}\) of \(K\) such that there is a prime \(\mathfrak{q}\) of \(L\) over \(\mathfrak{p}\) with Frobenius \(g\). In fact, the Dirichlet density of such primes \(\mathfrak{p}\) is the order of the conjugacy class of \(G\) divided by \(\shar G\).
Cf. Dirichlet density.
Let \(L/K\) be a nontrivial extension of number fields. Then there exist infinitely many primes of \(K\) which do not split completely in \(L\).
Class field axiom
With notation of Weil group, we say \(A\) satisfies the class field axiom if forevery cyclic extension \(L/K\) of finite subextensions of \(\bar{k}/ k\), \[\shar H^{i}_{T}(\Gal(L/K), A_{L}) = \begin{cases} [L:K] & i = 0 \\ 1 & i = -1 \end{cases} \]
Cohomology of local fields
We collect some result of cohomology of local fields here.
For Unramified case,
For any finite unramified extension \(L/K\) over local fields, the map \(\nm_{L/K}: \mathfrak{o}_{L}^{*} \to \mathfrak{o}_{K}^{*}\) is surjective.
For any finite unramified extension \(L/K\) of local fields, \(H^{i}_{T}(\Gal(L/K), \mathfrak{o}_{L}^{*}) = 1\) for all \(i \in \ZZ\).
For any finite unramified extension \(L/K\) over local fields, \(H^{2}(L/K)\) is cyclic of order \([L: K]\).
For cyclic case,
Let \(L/K\) be a finite Galois extension of local fields. Then there is an open, Galois-stable subgroup \(V\) of \(\mathfrak{o}_{L}\) as additive group such that \(H^{i}(\Gal(L/K), V) = 0\) for all \(i > 0\).
Let \(L/K\) be a finite Galois extension of local fields. Then there exists an open, Galois-stable subgroup \(W\) of \(\mathfrak{o}_{L}\) as multiplicative group such that \(H^{i}(\Gal(L/K), W) = 0\) for all \(i > 0\).
for \(L/K\) a acyclic extension of local fields, \(\shar H_{T}^{0}(\Gal(L/K), L^{*}) = [L:K]\).
For general case,
for any finite Galois extension \(L/K\) of local fields, the group \(H^{2}(\Gal(L/K), L^{*})\) has order at most \([L:K]\).
Let \(L/K\) be a finite Galois extension of local fields. Let \(M/K\) be an unramified extension of degree \([L:K]\). Then the image of \(H^{2}(L/K)\) in \(H^{2}(ML/K)\) contains the image of \(H^{2}(M/K)\) in \(H^{2}(ML/K)\). Consequently, the group \(H^{2}(\Gal(L/K), L^{*})\) contains a cyclic subgroup of order \([L:K]\).
Cohomology of group
We define the cohomology of the group to be \(H^{i}(G, M)\) the derived functor of \((\bullet)^{G}\). To compute it, we can use either Injective resolution or F-acyclic resolution.
Given a \(G\)-module \(M\), we can define \(G\)-module \(N^{i}\) for \(i \geq 0\) as the set of functions \(\phi: G^{i + 1} \to M\) with \(G\)-action \[(\phi^{g})(g_{0}, \cdots, g_{i}) = \phi(g_{0}g^{-1}, \cdots, g_{i}g^{-1})^{g}\] We have \(N^{i} = \Ind_{1}^{G} N_{0}^{i}\) for \(N_{0}^{i}\) consists of \(\phi(g_{0}, \cdots, g_{i}) = 0\) when \(g_{0} \neq e\). So \(N^{i}\) is Induced. Also we define the map \(\dif^{i}: N^{i} \to N^{i + 1}\) by \[(\dif^{i} \phi)(g_{0}, \cdots, g_{i + 1}) = \sum_{j = 0}^{i + 1} (-1)^{j} \phi(g_{0}, \cdots, \hat{g_{j}}, \cdots, g_{i + 1})\] With above definition, we have \(0 \to M \to N^{0} \to N^{1} \to \cdots\) exact, which is in fact acyclic resolution by Shapiro’s lemma.
There are some functoriality of group cohomology.
- Cohomology group has no nontrivial \(G\)-action.
- If \(H\) is a subgroup of \(G\), \(M\) a \(G\)-module, \(M'\) is \(M\) with \(H\)-action only, we have restriction homomorphism \[{\rm Res}:H^{i}(G, M) \to H^{i}(H, M')\]
- Let \(M\) be Ga \(\)-module, then we have corestriction map \[{\rm Cor}:H^{i}(H, M) \cong H^{i}(G, \Ind_{H}^{G} M) \to H^{i}(G, M)\]
- \({\rm Cor} \circ {\rm Res}\) acts as multiplication by \([G:H]\) on each cohomology group.
- Let \(H\) be a normal subgroup of \(G\). We have \(G/H\) acts on \(M^{H}\), and therefore inflation homomorphisms \[{\rm Inf}: H^{i}(G/H, M^{H}) \to H^{i}(G, M)\]
The group \(H^{i}(G, M)\) is the direct limit of \(H^{i}(G/H, M^{H})\) using the inflation homomorphisms.
the following proposition is called inflation-restriction exact sequence
Let \(G\) be a finite group and \(H\) be a normal subgroup, and \(M\) a \(G\)-module. If \(H^{i}(H, M) = 0\) for \(i = 1, \cdots, r - 1\), then the sequence \[0 \to H^{r}(G/H, M^{H}) \xrightarrow{{\rm Inf}} H^{r}(G, M) \xrightarrow{{\rm Res}} H^{r}(H, M)\] is exact.
The underlying theory is Spectral sequence.
If \(M/L/K\) is a tower of fields with \(M/K\) and \(L/K\) finite and Galois, the sequence \[0 \to H^{2}(L/K) \xrightarrow{{\rm Inf}} H^{2}(M/K) \xrightarrow{{\rm Res}} H^{2}(M/L) \] is exact.
Cf. G-module.
Coinvariant
See Augmentation ideal.
Conductor
In Kronecker-Weber theorem, the smallest number \(K \subset \QQ(\zeta_{n})\) is called the conductor of \(K/ \QQ\).
In Artin’s reciprocity law, the conductor of \(L/K\) is the smallest formal product \(\mathfrak{m}\) for which the reciprocity law holds.
Corestriction
See Cohomology of group.
TODO Dedekind domain
Referenced: Fractional ideal.
Decomposition group
Let \(L/K\) be field extension \(G\) the Galois group. Let \(\mathfrak{p}\) prime ideal of \(K\) and \(\tau\) prime ideal of \(L\) over \(\mathfrak{p}\). Then the decomposition group is the group \(G_{\tau} \subset G\) which consists of the stabilizer of \(\tau\) under the action of \(G\) on the primes above \(\mathfrak{p}\).
Dirichlet density
A set of primes \(S\) in a number field \(K\) has Dirichlet density \(d\) if \[\lim_{s \to 1^{+}} \frac{\sum_{\mathfrak{p} \in S} \nm(\mathfrak{p})^{-s}}{\log \frac{1}{s - 1}} = d\] This persumes the existence of the limit; otherwise, we have lower Dirichlet density and upper Dirichlet density.
Cf. Norm.
Discrete valuation
The Valuation is a discrete valuation if there is a \(\delta > 0\) such that \(1 - \delta < \abs{\alpha} < 1 + \delta\) implies \(\abs{\alpha} = 1\). After taking log and do some normalization, we get a morphism \[v: k^{\times} \to \ZZ\]
TODO Discriminant
Fractional ideal
A fractional ideal of a Dedekind domain \(A\) is a nonzero \(A\)-submodule \(\mathfrak{a}\) \(K\) such that \[d \mathfrak{a} \subset A\] for some nonzero \(d \in A\). With product, all the fractional ideal of \(A\) form a group called fractional ideal group.
Referenced: Norm.
Frobenius element
Let \(L\) be a finite Unramified extension of \(K\). Then \(L\) is Galois over \(K\) and \(\Gal(L/K)\) on \(\mathscr{O}_{L}\) defines an isomorphism \(\Gal(L/K) = \Gal(l/k)\) where \(l/k\) are the residue field. Therefore \(\Gal(L/K)\) is a cyclic group and generated by \(\sigma\) with \(\sigma \alpha \equiv \alpha^{q} \pmod{\mathfrak{m}_{L}}\) for \(\alpha \in \mathscr{O}_{L}\). \(\sigma\) is called Frobenius element and denoted by \(\Frob_{L/K}\).
In general, we have to choose a prime \(\mathfrak{p}\) of \(K\)and \(\mathfrak{q}\) prime above \(\mathfrak{p}\), then the element of the Decomposition group \(G_{\mathfrak{p}}\) such that \(gx \equiv x^{\shar(\mathfrak{o}_{K}/ \mathfrak{p})} \pmod{\mathfrak{q}}\). In general, Frobenius element only defined up to conjugation.
Frobenius reciprocity law
The following is Frobenius reciprocity law.
Let \(H\) be the a subgroup of \(G\), let \(M\) be a \(G\)-module and \(N\) be an \(H\)-module. Then there are natural isomorphisms \[\Hom_{G}(M, \Ind_{H}^{G} N) \cong \Hom_{H}(M,N)\] \[\Hom_{G}(\Ind_{H}^{G} N, M) \cong \Hom_{H}(N, M)\]
Cf. Induction.
Generalized ideal class group
Let \(\mathfrak{m}\) be a formal product of places of \(K\). Let \(J^{\mathfrak{m}}_{K}\) be the group of Fractional ideals of \(K\) which are coprime to each finite place of \(K\) occuring in \(\mathfrak{m}\). Let \(P_{K}^{\mathfrak{m}}\) be the group of principal fractiona ideals generated by elements \(\alpha \in K\) such that
- for \(\mathfrak{p}^{e} \mid \mathfrak{m}\) finite, \(\alpha \equiv 1 \pmod \mathfrak{p}^{e}\).
- For every real place \(\tau\) in \(\mathfrak{m}\), \(\tau(\alpha) > 0\).
Then the ray class group \({\rm Cl}^{\mathfrak{m}}(K)\) is defined as the quotient \(J^{\mathfrak{m}}_{K} / P^{\mathfrak{m}}_{K}\). A quotient of a ray class group is called a generalized ideal class group.
Cf. Ideal class.
G-extension
If \(G\) a group, a G-extension of a field \(K\) is a Galois extension of \(K\) with Galois group \(G\).
G-module
Let \(G\) be a finite group. A (right) G-module is an abelian group \(A\) equipped with a right \(G\)-action.
Given a \(G\)-module \(M\), we denote by \(M^{G}\) the abelian group of \(G\)-invariant elements of \(G\). The functor \(M \to M^{G}\) is left exact.
Consider exact sequence \(0 \to \ZZ / p \ZZ \to \ZZ/ p^{2} \ZZ \to \ZZ / p \ZZ \to 0\), for \(G = \ZZ / p \ZZ\), which acts on the middle by \(a^{g} = a(1 + pg)\). After applying \((\bullet)^{G}\), the sequence is not right exact.
For \(G\)-module of Profinite group \(G\), we require that \(M\) is topological group and the action \(G \times M \to M\) is continuous.
Induced
A \(G\)-module is called induced if it is of this form \(\Ind_{1}^{G} N\). for some \(N\).
The following is a corollary for Shapiro’s lemma.
if \(M\) is an induced \(G\)-module, then \(M\) is acyclic.
Herbrand quotient
Let \(G\) be a finite cyclic group and let \(M\) be a \(G\)-module. If the group \(H_{T}^{i}(G, M)\) are finite, we define the Herbrand quotient as the ratio \[h(M) = \shar H^{0}_{T}(G, M) / \shar H_{T}^{-1}(G, M)\]
By periodicity theorem of Tate cohomology group, for exact sequence \(0 \to M' \to M \to M'' \to 0\), we have \(h(M) = h(M') h(M'')\).
A interesting fact is the following.
If \(M\) is finite, then \(h(M) = 1\).
Henselian valuation
With the notation of Weil group, a henselian valuation of \(A_{k}\) with respect to \(d\) is a homomorphism \(v: A_{k} \to \hat{Z}\) such that
- the group \(Z = \im(v)\) contains \(\ZZ\) and staisfies \(Z/nZ \cong \ZZ/ n \ZZ\) for all positive integer \(n\);
- for every finite extension \(K\) of \(k\), \(v(\nm_{K/k}A_{K}) = f_{K/k} Z\).
for any finite subextension \(K\) of \(\bar{k}/k\), define the unit group \(U_{K}\) as the set of \(u \in A_{K}\) with \(v_{K}(u) = 0\). We say \(\pi \in A_{K}\) is a uniformizer for \(K\) if \(v_{K}(\pi) = 1\).
Hilbert class fields
Let \(L\) be the maximal Unramified abelian extension of a number field \(K\). Then \(L/K\) is finite, and its Galois group is isomorphic to the ideal class group \({\rm Cl}(K)\) of \(K\). The field \(L\) is called Hilbert class field of \(K\).
Homology of group
We define the homology of groups to be the left derived functor of Coinvariant.
Cf. Cohomology of group.
TODO Ideal class
Referenced: Finiteness of class group.
Idèle
Let \(K\) be a number field and let \(\mathbb{A}_{K}\) be the ring of Adèles associated to \(K\). We define the group of idèles \(I_{K}\) associated to \(K\) as the gorup of units of the ring \(\mathbb{A}_{K}\). In fact \(I_{K}\) is Restricted topological product of \((K_{v}^{*}, \mathbb{o}_{K_{v}}^{*})\).
\(I_{K} \ito \mathbb{A}_{K}\) is continuous, but the topology of \(I_{K}\) does not coincide with the subspace topology for the embedding! For example \(I_{K,S}\) is open in \(I_{K}\) but not the intersection with an open subset of \(\mathbb{A}_{K}\).
We have \(I_{K} = \cup_{S} I_{K,S}\), where \(S\) is finite set and \(I_{K,S}\) denote the element \(x_{v} \in \mathbb{o}_{K_{v}}^{*}\) for each finite place \(v \in S\). Elements of \(I_{K,S}\) called S-units. (Cf. S-integer)
For each \(\alpha \in K^{*}\), the principal adèle \(\alpha \in \mathbb{A}_{K}\) is an idèle, so we have an embedding \(K^{*} \to I_{K}\). We refer to elements of this embedding principal idèles. Define the idèle class group of \(K\) as the quotient \(C_{K} = I_{K}/K^{*}\).
We have surjection \(C_{K} \to {\rm Cl}(K)\) with kernel \(I_{K,S}K^{*}/K^{*}\).
We have well defined norm \(\abs{\cdot}:C_{K} \to \RR_{+}^{*}\) derived from \(\mathbb{A}_{K}\). Let \(C_{K}^{0}\) denote the kernel of this map.
The group \(C_{K}^{0}\) is compact.
The class group \({\rm Cl}(K)\) of \(K\) is finite.
The following is the famous Dirichlet’s unit theorem
The group of units of \(\mathb{o}_{K}\) fits into an exact sequence \[0 \to \mu_{K} \to \mathbb{o}_{K}^{*} \to \ZZ^{r + s - 1} \to 0\] in which \(\mu_{K}\) is the group of unity of \(K\) and \(r\) ans \(s\) are number of real and complex places, respectively. More generally, for any finite set \(S\) of places containing all infinite places, the group of units of the ring \(\mathbb{o}_{K,S}\) of \(S\)-integers fits into an exact sequence \[0 \to \mu_{K} \to \mathbb{o}^{*}_{K,S} \to \ZZ^{\shar S -1} \to 0\]
Induction
If \(H\) is a subgroup of \(G\) and \(M\) is an \(H\)-module, we define the induction of \(M\) from \(H\) to \(G\) to be \(\Ind_{H}^{G} M = M \otimes_{\ZZ[H]} \ZZ[G]\). We may also identify \(\Ind_{H}^{G} M\) with the set of functions \(\phi: G \to M\) such that \(\phi(gh) = \phi(g)^{h}\) for \(h \in H\).
Inflation map
See Cohomology of group.
Inertial degree
See Weil group.
Inertia group
See Weil group.
Kronecker-Weber theorem
The Kronecker-Weber theorem is the following
If \(K/ \QQ\) is a finite ableian extension, then \(K \subset \QQ(\zeta_{n})\) for some positive integer \(n\).
We also have a local version, called local Kronecker-Weber theorem.
If \(K/ \QQ_{p}\) is a finite ableian extension, then \(K \subset \QQ_{p}(\zeta_{n})\) for some positive integer \(n\), where \(\zeta_{n}\) is a primitive \(n\)-th root of unity.
Kummer theory
The following theorem is key in Kummer theory of ableian extensions.
If \(\zeta_{n} \in K\), then every \(\ZZ/n \ZZ\) extension of \(K\) is of the form \(K(\alpha^{1/n})\) for some \(\alpha \in K^{*}\) with the property that \(\alpha^{1/d} \not \in K\) for any proper divisor \(d\) of \(n\) and vice versa.
L-function
Let \(\K\) be a number field \(\mathfrak{m}\) formal product of Places of \(K\). Let \(\chi_{\mathfrak{m}}: {\rm Cl}^{\mathfrak{m}}(K) \to \CC^{*}\) be a character. Then we can extend \(\chi_{\mathfrak{m}}\) to a function on all ideal of \(K\) by declaring its value to be \(0\) on ideals not coprime to \(\mathfrak{m}\). Then we define the L-function \[L(s, \chi_{\mathfrak{m}}) = \prod_{\mathfrak{p} \not \div \mathfrak{m}}(1 - \chi(\mathfrak{p}) \nm(\mathfrak{p})^{-1})^{-1}\] which convergent absolutely for \({\rm Re}(s) > 1\). In fact, we have the following theorem
If \(\chi_{\mathfrak{m}}\) is not trivial, then \(L(s, \chi_{\mathfrak{m}})\) extends to an analytic function on \(\CC\).
We also have nonvanishing theorem
If \(\chi_{\mathfrak{m}}\) is not the trivial character, then \(L(1, \chi_{\mathfrak{m}}) \neq 0\).
Cf. Norm.
Langlands correspondence
Langlands prgram
As far as I know there are several parts of Langlands program, namely reciprocity conjecture and functoriality conjecture. The following is the reciprocity conjecture
Suppose \(E\) is a finite Galois extension of \(F\) with Galois group \(G = \Gal(E/F)\), and \(\sigma: G \to \GL_{n}(\CC)\) is an irreducible representation of \(G\). Then there exists an automorphic cuspidal representation \(\pi_{\sigma}\) on \(\GL_{n}\) over \(F\) such that \(L(s, \pi_{\sigma}) = L(s, \sigma)\).
And the functoriality conjecture
Suppose \(G\) and \(G'\) are reductive groups, and \(\rho: ^{L}G \to ^{L}G'\) is an \(L\)-homomorphism. Then to each automorphic representation \(\pi = \otimes \pi_{v}\) of \(G\), there is an automorphic representation \(\pi' = \otimes \pi'_{v}\) of \(G'\) such that for unramified \(v\), \(t(\pi'_{v})\) is the conjugacy class in \(^{L}G'\) which contains \(t(\pi_{v})\). Moreover, for any finite dimensional representation \(r'\) of \(^{L}G'\), we have \[L(s, \pi', r') = L(s, \pi, r' \circ \rho)\] Here \(^{L}G\) denote the Langlands dual group.
The functoriality conjecture implies reciprocity conjecture.
Local existence theorem
The norm groups in \(K^{\times}\) are exactly the open subgroups of finite index.
Cf. Norm group.
Local reciprocity map
For every nonarchimedian local field \(K\), there exists a unique homomorphism \[\phi_{K}: K^{\times} \to \Gal(K^{ab}/K)\] with following properties a. For every prime element \(\pi\) of \(K\) and every finite unramified extension \(L\) of \(K\), \(\phi_{K}(\pi)\) acts on \(L\) as \(\Frob_{L/K}\). b. For every finite ableian extension \(L\) of \(K\), the \(\nm_{L/K}(L^{\times})\) is contained in the kernel of \(a \to \phi_{K}(a)|_{L}\) and \(\phi_{K}\) induces an isomorphism \[\phi_{L/K}:K^{\times}/\nm_{L/K}(L^{\times}) \to \Gal(L/K)\] In particular, \((K^{\times}: \nm_{L/K}(L^{\times})) = [L : K]\).
Here \(\phi_{K}\) and \(\phi_{L/K}\) are called local Artin maps or local reciporicity maps and \(\phi_{L/K}\) is also called norm residue map or symbol.
By local existence theorem, we have local existence theorem
For every finite (not necessarily abelian) extension \(L\) of \(K\), \(\nm_{L/K}(L^{*})\) is an open subgroup of \(K^{*}\) of finite index. Conversely, for every (open) subgroup \(U\) of \(K^{*}\) of finite index, there exists a finite abelian extension \(L\) of \(K\) such that \(U = \nm_{L/K} L^{*}\).
To see \(\nm_{L/K} L^{*}\) is norms of which abelian extension, we have norm limitation theorem.
Let \(M\) be the maximal abelian subextension of \(L/K\). Then \(\nm_{L/K} L^{*} = \nm_{M/K} M^{*}\).
Maximal abelian extension
Let \(\QQ_{p}^{cycl}\) be the field generated over \(\QQ\) by all roots of unity. Then \(\QQ_{p}^{cycl}\) is the maximal abelian extension of \(\QQ_{p}\).
on p. 172
Norm
Let \(L/K\) be finite field extension, for \(\alpha \in L\), we have norm \(\nm(\alpha)\) in \(K\) defined as \(\det(a_{ij})\), where \(\alpha e_{i} = \sum a_{ij}e_{j}\) and \(\{e_{1}, \cdots, e_{n}\}\) is a basis for \(L\) over \(K\).
We can also consider the norm map \(\nm: \id(B) \to \id(A)\), where \(\id\) denote the Fractional ideal group.
In group theory, we define norm to be \[\nm_{G}(m) = \sum_{g \in G} m^{g}\] which induces a homomorphism \[\nm_{G}: H_{0}(G, M) \to H^{0}(G, M)\]
In abstract class field theory, with the notation of Weil group, we define the norm map \(\nm_{L/K}: A_{L} \to A_{K}\) by \(\nm_{L/K}(a) = \prod_{g} a^{g}\), where \(g\) runs over a set of right coset representatives of \(G_{L}\) in \(G_{K}\).
For Adèles, we can also have norm map, for \(L/K\) an extension of number fields, we define the norm map \(\nm_{L/K}: I_{L} \to I_{K}\) by \[\nm_{L/K}(x) \to \prod_{g} x^{g}\] where \(g\) runs over coset representatives of \(\Gal(\bar{K}/L)\) in \(\Gal(\bar{K}/K)\). Similar for trace map \(\tr_{L/K}: \mathbb{A}_{L} \to \mathbb{A}_{K}\).
Norm group
A subgroup of \(K^{\times}\) is called a norm group if it is of the form \(\nm(L^{\times})\) for some finite abelian extension \(L\).
Referenced: Local existence theorem.
Place
A place of a number field \(K\) is a equivalence class of nontrivial Absolute values on \(K\).
Principal ideal theorem
Principal ideal theorem concerns the ideals of Hilbert class fields.
Let \(L\) be the Hilbert class field of the number field \(K\). Then every ideal of \(K\) becomes principal in \(L\).
Profinite group
A profinite group is a topological group which is Hausdorff and compact, and which admits a basis of neighborhoods of the identity consisting of normal groups. More explicitly, a profinite group is a group \(G\) plus a collection of subgroups of \(G\) of finite index as open subgroups, such that the intersection of two open subgroups is open, but the intersection of all of the open subgroup is trivial.
The profinite group can also be defined as limits. Suppose we are given a partially ordered set \(I\), a family \(\{G_{i}\}_{i \in I}\) of finite groups and a map \(f_{ij}: G_{i} \to G_{j}\) for each pair \((i, j) \in I \times I\) such that \(i > j\). Then there exists a profinite group \(G\) with open subgroups \(H_{i}\) for \(i \in I\) such that \(G/H_{i} \cong G_{i}\) in a manner compatible with the \(f_{ij}\), the limit of system.
So if \(L/K\) Galois extension but not necessarily finite, we make \(G = \Gal(L/K)\) into a profinite group by declaring that the open subgroups of \(G\) are precisely \(\Gal(L/M)\) for all finite extensions \(M\) of \(K\). In fact, we have following Galois correspondence
Let \(L/K\) be a Galois extension. Then there is a correspondence between (Galois) subextension of \(M\) of \(L\) and (normal) closed subgroups \(H\) of \(\Gal(L/K)\), given by \[H \to {\rm fix} H, \; M \to \Gal(L/M)\]
Ramification degree
See Inertia group.
Ramification index
Let \(L/K\) be an extension of number fields. Let \(\mathfrak{p}\) be a nonzero prime ideal in the integer of rings \(\mathfrak{o}_{K}\) of \(K\), and \[\mathfrak{p} \mathfrak{o}_{L} = \prod_{i=1}^{n} \mathfrak{P}_{i}^{e_{i}}\] for some prime ideal \(\mathfrak{P}_{i} \in \mathfrak{o}_{L}\). Then the natural number \(e_{i}\) is called the ramification index of \(\mathfrak{P}_{i}\) over \(\mathfrak{p}\), denoted by \(e(\mathfrak{P}_{i}/ \mathfrak{p})\). If \(e_{i} > 1\), we say that ideal \(\mathfrak{p}\) is ramified in \(L\).
Ramification index can be generalized to local fields.
Ramified
See Ramification index.
Ray class field
We say \(L/K\) is the ray class field corresponding to the product \(\mathfrak{m}\) if \(L/K\) has Conductor dividing \(\mathfrak{m}\) and the map \(J_{K}/J_{K}^{\mathfrak{m}} \to \Gal(L/K)\) is an isomorphism.
There is the existence theorem for ray class field.
Every formal product \(\mathfrak{m}\) of \(K\) has a ray class field.
Cf. Ray class group.
Ray class group
See Generalized ideal class group.
Reciprocity map
If \(A\) satisfies Class field axiom, \(v\) is henselian valuation of \(A_{k}\) with respect to \(d\). Let \(L/K\) be a Galois extension of finite subextensions of \(\bar{k}/k\). Let \(H\) be the semigroup of \(g \in \Gal(L^{ur}/K)\) such that \(d_{K}(g)\) is a positive integer. Define the map \[r' : H \to A_{K} / \nm_{L/K} A_{L}\] by for \(g \in \Gal(L^{ur}/K)\), \(M\) the fixed field of \(g\) set \(r'(g) = \nm_{M/K}(\pi_{M})\) for some uniformizer \(\pi_{M}\) of \(M\). \(r'\) induces a homomorphism \(r = r_{L/K}: \Gal(L/K) \to A_{K} / \nm_{L/K} A_{L}\) and is called reciprocity map.
For each Galois extension \(L/K\) of finite subextension of \(\bar{k}/k\), the homomorphism \(r_{L/K}\) induces an isomorphism \(\Gal(L/K)^{ab} \to A_{K} / \nm_{L/K}A_{L}\).
Under the hypothesis of the theorem, let \(L_{1}/K\) and \(L_{2}/K\) be abelian extensions of finite subextensions of \(\bar{k}/k\). If \(\nm_{L_{1}/K} A_{L_{1}} = \nm_{L_{2}/K} A_{L_{2}}\), then \(L_{1} = L_{2}\).
TODO Residue class degree
Restricted topological product
Let \(I\) be an index set. For each \(i \in I\), let \(G_{i}\) be a set and let \(H_{i}\) be a set of \(G_{i}\). The restricted direct product \(G\) of the pairs \((G_{i}, H_{i})\) is the set of tuples \((g_{i})_{i = 1}^{\infty}\) such that \(g_{i} \in H_{i}\) for all but finitely many indices \(i\).
Restriction
See Cohomology of group.
Riemann zeta function
\[\zeta(s) = 1 + \frac{1}{2^{s}} + \frac{1}{3^{s}} + \cdots = \prod_{p \text{ prime}} \frac{1}{1 - p^{-s}}\] The function can be extend as a meromorphic function on \(\CC\).
Rosseta stone in mathematics
The similarity over number fields, function fields, algebraic curves over \(\CC\).
Referenced: Personal Thoughts.
Shapiro’s lemma
The following is Shapiro’s lemma.
If \(H\) is a subgroup of \(G\) and \(N\) is an \(H\)-module, then there is a canonical isomorphism \(H^{i}(G, \Ind_{H}^{G} N) \to H^{i}(H, N)\). In particular, \(N\) is an acyclic \(H\)-module if and only if \(\Ind_{H}^{G}(N)\) is an acyclic \(G\)-module.
Cf. Induction.
S-unit
Cf. S-integer.
Tamely ramified
See Unramified.
Tate cohomology group
We define the Tate cohomology groups to be \[H^{i}_{T} = \begin{cases} H^{i}(G, M) & i > 0 \\ M^{g} / \nm_{G}(M) & i = 0 \\ \ker(\nm_{G})/M I_{G} & i = -1 \\ H_{-i - 1}(g, M) & i < -1 \end{cases} \]
It is called cohomology group because it induces long exact sequence.
We have periodicity theorem for cohomology of cyclic groups.
Let \(G\) be a finite cyclic group and \(M\) a \(G\)-module. Then there is a functorial isomorphism \(H_{T}^{i}(G, M) \to H_{T}^{i + 2}(G, M)\) for all \(i \in \ZZ\); moreover, these isomorphisms are all determined by the choice of generator of \(G\).
Tate’s theorem
Tate’s theorem refers to the following
Let \(G\) be a finite group and let \(M\) be a \(G\)-module. Suppose that for all subgroups \(H\) of \(G\) (including \(G\) itself), \(H^{1}(H,M) = 0\) and \(H^{2}(H, M)\) is cyclic of order \(\shar H\). Then there are isomorphisms \(H_{T}^{i}(G, \ZZ) \to H^{i + 2}_{T}(G, M)\) which are canonical up to a choice of generator of \(H^{2}(G, M)\).
Cf. Tate cohomology group, Cohomology of local fields.
Totally ramified
See Unramified.
Transfer map
Let \(G\) be a finite group and \(H\) subgroup (not necessarily normal). Let \(g_{1}, \cdots, g_{n}\) be left coset representatives of \(H\) in \(G\). Let \(\phi(g) = g_{i}\) if \(g \in g_{i}H\). Then we define \(V(g) = \prod_{i = 1}^{n} \phi(g g_{i})^{-1}(g g_{i})\). The induced map \(V: G^{ab} \to H^{ab}\) is called the tranfer map.
Uniformizer
See Henselian valuation.
Unit group
See Henselian valuation.
If \(A\) satisfies Class field axiom, \(v\) is henselian valuation of \(A_{k}\) with respect to \(d\). Then we have following proposition.
Let \(L/K\) be an unramified extension of finite subextensions of \(\bar{k}/k\).
- The group \(H_{T}^{i}(\Gal(L/K), U_{L})\) are all trivial.
- The group \(H_{T}^{0}(\Gal(L/K), A_{L})\) is cyclic, generated by an uniformizer \(\pi_{L}\) of \(L\).
Cf. Uniformizer, Unramified.
Unramified
Let \(L/K\) be an extension of finite extensions of \(\QQ_{p}\). Let \(\mathfrak{o}_{L}, \mathfrak{o}_{K}\) be the integral closure of \(\ZZ_{p}\) in \(K, L\). We say \(L/K\) is unramified if the maximal ideal of \(\mathfrak{o}_{K}\) generates the maximal ideal of \(\mathfrak{o}_{L}\).
For every extension \(L/K\) there exists a maximal subextension of \(L/K\) which is unramified, denoted by \(U\). If this is \(K\), we say \(L/K\) is totally ramified.
If \([L:U]\) is not divisible by \(p\), then \(L/K\) is tamely ramified.
The above definition can be generalized to global fields by specifiying the prime ideal.
In class field theory, the phrase \(L/K\) is unramified means that \(L/K\) is unramified over all finite places and every real embedding of \(K\) extends to a real embeddings of \(L\).
An unramified extension can be nonabelian. It is related to class field tower over \(K\).
Valuation
A valuation \(\abs{\cdot}\) on a field \(k\) is a function defined on \(k\) with values in the non-negative real numbers satisfying the following axioms.
- \(\abs{\alpha} = 0\) if and only if \(\alpha = 0\).
- \(\abs{\alpha \beta} = \abs{\alpha} \abs{\beta}\).
- There is a constant \(C\) such that \(\abs{1 + \alpha} \leq C\) whenever \(\alpha \leq 1\).
There always exists trival valuation that \(\abs{\alpha} = 1\) for all \(\alpha \neq 0\).
Two valuations are called equivalent if there \(c > 0\) such that \(\abs{\alpha}_{2} = \abs{\alpha}_{1}^{c}\).
Referenced: Discrete valuation.
Weil group
Let \(k\) be field, and \(\bar{k}\) an algebraic extension. Put \(G = \Gal(\bar{k}/k)\) and \(A\) be a \(G\)-module. Then for subextension \(K\) of \(\bark{k}/k\), define \(A_{K} = A^{\Gal(\bar{k}/K)}\).
Let \(d: G \to \hat{\ZZ}\) be a continuous surjective homomorphism. The Weil group of \(k\) is the subgroup \(d^{-1}(\ZZ)\) of \(G\).
The inertia group \(I_{k}\) is the kernel of \(d\). And maximal unramified extension \(k^{ur}\) of \(k\) to be the fixed field of \(I_{k}\). For subextension \(K\) of \(\bar{k}/k\), put \(I_{K} = G_{K} \cap I_{k}\) and let \(K^{ur} = k^{ur} K\). We say an extension \(L/K\) of subextension of \(\bar{k}/k\) is unramified if \(L \subset K^{ur}\).
Put \(d_{K} = \frac{1}{ [\hat{\ZZ}: d(G_{K})]} d\), then \(d_{K}\) induces isomorphism \(\Gal(K^{ur}/K) \cong \hat{ZZ}\). Given a finite extension \(L/K\) of subextensions of \(\bar{k}/k\), define the inertia degree \[f_{L/K} = [d(G_{K}) : d(G_{L})]\] and the ramification index \[e_{L/K} = [I_{K}: I_{L}]\]
we have \[e_{L/K} f_{L/K} = [L:K]\]
Zeta functions
Let \(K\) be a number field. The Dedekind zeta function \(\zeta_{K}(s)\) is defined for \({\rm Re}(s) >1\) \[\zeta_{K}(s) = \prod_{\mathfrak{p}}(1 - \nm(\mathfrak{p})^{-s})^{-1}\] where \(\mathfrak{p}\) runs over the nonzero prime ideals of \(\mathfrak{o}_{K}\).
The function \(\zeta_{K}(s)\) extends to a meromorphic function on \(\CC\) whose only pole is a simple pole at \(s = 1\).
Cf. Riemann zeta function, Norm.
Arithmetic Geometry
Absolute height
See Height.
Absolute value
An absolute value on a field \(k\) is a real-valued function \[\abs{\cdot}: k \to \linterval{0}{\infty}\] with the following properties
- \(\abs{x} = 0\) if and only if \(x = 0\).
- \(\abs{xy} = \abs{x} \abs{y}\).
- \(\abs{x + y} \leq \abs{x} + \abs{y}\).
The absolute value is said to be nonarchimedean if it satisfies \[\abs{x + y} \leq \max \{ \abs{x}, \abs{y}\}\]
Referenced: Degree formula, Local degree, Nonarchimedean, Normalized absolute value.
Degree formula
Let \(k' / k\) be an extension of number fields, and let \(v \in M_{k}\) be an Absolute value on \(k\). Then \[\sum_{w \in M_{k'}, w | v} [k'_{w} : k_{v}] = [k' : k]\] where \(k_{v}\) is the \(v\) completion of \(k\).
Dirichlet theorem
Let \(\alpha \in \RR\) with \(\alpha \not \in \QQ\). Then there are infinitely many rational number \(p/q \in \QQ\) such that \[\abs{\alpha - \frac{p}{q}} < \frac{1}{q^{2}}\]
The constant on the right hand side can be refined to \(\frac{1}{\sqrt{5}q^{2}}\), which can not be further required for \(\alpha = \frac{-1 + \sqrt{5}}{2}\).
Referenced: Roth’s theorem.
Elliptic curve
An elliptic curve \(E\) over \(K\) is a nonsingular projective curve of genus \(1\), which comes equipped with a rational point \(\OO \in E(K)\) the origin. A morphism \(E \to E'\) between elliptic curves over \(K\) is a morphism of \(K\)-schemes which preserves the origin. It is an isomorphism if it is an isomorphism of \(K\)-schemes.
The following theorem shows the elliptic curve can always be realized as a plane cubic curve.
Let \(E/K\) be an elliptic curve. Then \(E\) is isomorphic to a plane cubic curve with affine equation \[y^{2} + a_{1} xy + a_{3}y = x^{3} + a_{2}x^{2} + a_{4}x + a_{6}\] for some \(a_{1}, \cdots, a_{4}, a_{6} \in K\) such that the above equation has no singularities.
Referenced: Origin, Group law, Isogeny.
Origin
See Elliptic curve.
Group law
We write \(\pic^{\circ} X\) for the subgroup of divisor classes of degree \(0\).
This is a special case of the Jacobian variety.
Let \(E\) be an elliptic curve over \(K\). There is a bijection \(E(K) \cong \pic^{\circ}E\) sending \(P\) ot the class \((P) - (O)\).
Cf. Elliptic curve.
The group is defined by \(P + Q = R\), where \((P) + (Q) = ( R) + (O)\).
TODO Dual
Isogeny
An isogeny is a morphism between Elliptic curves which is finite.
Referenced: Isogeny.
Riemann hypothesis
Let \(E/ \mathbb{F}_{q}\) be an elliptic curve, and define \(a(E) = q + 1 - \shar(\mathbb{F}_{q})\). Then \(\abs{a} \leq 2 \sqrt{q}\).
Tate module
Let \(l\) be a prime number unequal to the characteristic of \(K\). The Tate module of \(E\) is the inverse limit \[T_{l}E = \varprojlim E(\bar{K})[l^{n}]\] A free \(\ZZ_{l}\)-module of rank \(2\). The rational Tate module is \(V_{l}E = T_{l}E \otimes_{\ZZ_{l}} \QQ_{l}\). Here \(E(\bar{K})[m]\) denote the number of \(m\) torsion points of \(E(\bar{K})\).
Referenced: Tate’s isogeny theorem.
Tate’s isogeny theorem
Let \(E\) and \(E'\) be elliptic curves over a finite field \(K\). The map \[\Hom(E, E') \otimes_{Z} \QQ_{l} \to \Hom_{G_{K}}(V_{l}E, V_{l}E')\] is an isomorphism. Here \(G_{K}\) is the absolute Galois group of \(K\).
Cf. Tate module.
Mordell-Weil theorem
The first version is weak Mordell-Weil theorem.
Let \(K\) be a number field, let \(E/K\) be an elliptic curve, and let \(m \geq 2\). The group \(E(K)/mE(K)\) is finite.
Then we lead to (full) Mordell-Weil theorem.
\(E(K)\) is finitely generated.
The weak Mordell-Weil theorem do not implies Mordell-Weil theorem, for it doesn’t exclude case for example \(E(K) = \QQ / \ZZ\).
Finiteness of class group
There are finitely many ideal classes in \(K\).
Cf. Ideal class.
Finiteness of point under height
The following theorem shows some finiteness of points less than a given height.
For any number \(B, D \geq 0\), the set \[\{P \in \PP^{n}(\bar{\QQ}) \mid H(P) \leq B \text{ and } [\QQ(P) : \QQ] \leq D\}\] is finite. In particular, when \(k\) is fixed, the set \(\{P \in \PP^{n}(k) \mid H_{k}(P) \leq B\}\) is finite.
This implies the Kronecker’s theorem.
Let \(k\) be a number field, and \(P = (x_{0}, \cdots, x_{n})\). Fix any \(i\) with \(x_{i} \neq 0\). Then \(H(P) = 1\) if and only if the ratio \(x_{j}/ x_{i}\) is a root of unity or zero for every \(0 \leq j \leq n\).
Finiteness of unit group
The abelian group \(\OO_{K,S}\) is finitely generated.
Cf. S-integer.
Height
Let \(k\) be a number field and let \(P = (x_{0}, x_{1}, \cdots, x_{n}) \in \PP^{n}(k)\) be a point whose homogeneous coordinates are chosen in \(k\). The height is the quantity \[H_{k}(P) = \prod_{v \in M_{k}} \max \{\norm{x_{0}}_{v}, \norm{x_{1}}_{v}, \cdots, \norm{x_{n}}_{v}\}\] And define the logarithmic height by \[h_{k} = \log H_{k}(P)\] Cf. Normalized absolute value.
We have preceding formula for height in extension field
If \(k\) be a number field and \(k'/k\) a finite field extension. Then \[H_{k'}(P) = H_{k}(P)^{[k':k]}\]
By above lemma, we can define the absolute height on \(\PP^{n}\) by \[H: \PP^{n}(\bar{Q}) \to \linterval{0}{\infty}\] \[H(P) = H_{k}(P)^{1/[k: \QQ]}\] where \(P \in \PP^{n}(k)\). The absolute logarithmic height is defined similarly.
We can extend the definition of height to varieties. Let \(\phi: V \to \PP^{n}\) is a morphism, then we can define \[h_{\phi}(P) = h(\phi(P))\] The definition of this height is dependent on the choice of the morphism \(\phi\).
Referenced: Absolute height.
TODO Jacobian variety
Referenced: Group law.
Local degree
Let \(v \in M_{k}\) be an Absolute value on number field \(k\). The local degree of \(v\) is the number \[n_{v} = [k_{v} : \QQ_{v}]\]
Nonarchimedean
See Absolute value.
Normalized absolute value
Let \(v \in M_{k}\) be an Absolute value on number field \(k\). The normalized absolute value of \(v\) associated to \(v\) is \[\norm{x}_{v} = \abs{x}_{v}^{n_{v}}\]
For normalized absolute value, we have the product formula, for \(x \in k^{* }\), we have \[\prod_{v \in M_{k}} \norm{x}_{v} = 1\]
Referenced: Height.
Roth’s theorem
Let \(\alpha \in \bar{K}\), and let \(v \in S_{K}\). Extend \(\abs{\cdot}_{v}\) to an absolute value \(\abs{\cdot}_{v}\) on \(K(\alpha)\). For all \(\epsilon > 0\) and every \(C > 0\), the inequality \[\abs{\alpha - x}_{v} < \frac{C}{H_{K}(x)^{2 + \epsilon}}\] has only finitely many solutions in \(x \in K\).
Cf. Dirichlet theorem.
S-integer
The ring of S-integers of \(k\) is defined to be \[R_{S} = \{x \in k \mid \abs{x}_{v} \leq 1 \text{ for all } v \in M_{k}, v \not \in S\}\]
We can also characterize the rings of integers of \(k\) by \(M_{k}^{\infty}\)-integers of \(k\).
Referenced: S-unit, Finiteness of unit group.
Bibliography
[steinberg2012] Steinberg, Representation Theory of Finite Groups: An Introductory Approach, Springer (2012). ↩
[kirillov2016] Kirillov, Quiver Representations and Quiver Varieties, American Mathematical Society (2016). ↩
[dieck2008] tom Dieck, Algebraic Topology, European Mathematical Society (2008). ↩
[CLS2011] Cox, Little & Schenck, Toric Varieties, American Mathematical Society (2011). ↩
[milne2017] Milne, Algebraic Groups: The Theory of Group Schemes of Finite Type over a Field, Cambridge University Press (2017). ↩
[sernesi2006] Sernesi, Deformations of Algebraic Schemes, Springer Berlin Heidelberg (2006). ↩
[nakajima1999] Nakajima, Lectures on Hilbert Schemes of Points on Surfaces, American Mathematical Society (1999). ↩
[milne2020a] @miscMilne2020a, title = Exercises of Algebraic Number Theory (v3.08), author = Milne, J. S., year = 2020 ↩
[kedlaya2021] Kedlaya, Note on Class Field Theory, (2021). ↩