我本科读的是生物专业,研究生转到了数学专业。在本科毕业的班级聚餐上,同学问我之后会做什么方向,我回答了代数几何。大家一脸茫然地问什么是代数几何。我尝试地解释了一下说的也不是很清楚。前几天,高中同学聚餐时,听说我现在在做代数几何,我又被问到了什么是代数几何这个问题,我只好尴尬地笑了笑。为了避免以后遇到相似的尴尬,我决定写下这篇文章,以在被提问时能够直接把链接甩在别人的脸上作为回答。
从经典的代数几何来说,代数几何是研究代数簇的学问。那什么是代数簇呢?所谓代数簇就是多项式方程的一个零点集(更准确地说是局部像多项式方程零点集的空间),比如下图中就展示了三个不同的代数簇,分别是 \(x^{2} + y^{2} - 1 = 0\), \(y - x = 0\), \(y = x^{2}\)。所谓代数几何研究的就是这样的一些几何对象。
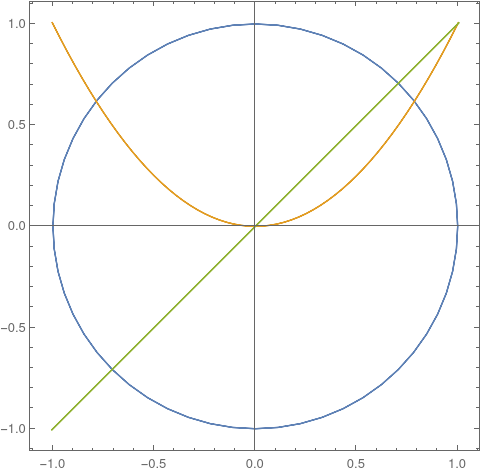
既然知道了是什么,那我们就可以问为什么要进行代数几何的研究。最粗暴的回答是,因为我们可以。在微积分中,我们可以用微分和积分来研究包括切线在内的诸多的几何问题。现在的微分几何建立在流形的基础之上,比如上图的三条曲线都是流形的例子。事实上最简单的流形的例子几乎都是由多项式方程的零点给出的,因此,代数簇在几何中是一个非常常见的对象,值得进行进一步的研究。而由于代数簇是使用多项式定义的,因此我们可以采用代数的方法进行研究,代数几何也就应运而生了。
事实上代数几何相比于微分几何,也有一些好处。最明显的一点,在于使用代数几何我们可以更好地研究一些具有奇点的几何对象。比如下面的这张图所展示的一条曲线,\(y^{2} = x^{3} + x^{2}\)。这条曲线在 \((0, 0)\) 点,有多重根,所以存在奇性。如果采用一般的微积分(微分几何)的方法进行研究,那在这个点附近就会出现问题。而使用代数的方法就能够更好地解释奇点的问题。
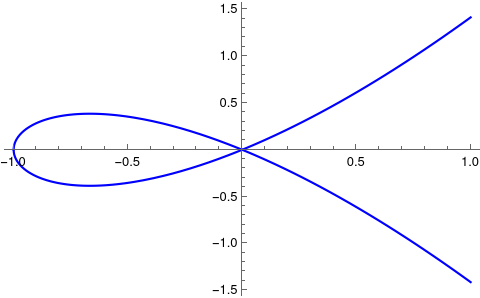
不太明显的一点在于,使用代数的方法能够以更加内禀的方式来描述一些几何的问题。比如我们考虑一条曲线 \(y = x^{2}\) 和直线 \(y = a\) 的交点。我们考虑 \(x,y \in \CC\) 的情况。我们知道,如果 \(a \neq 0\),那我们有两个不同的交点,而如果 \(a = 0\),那我们就有一个二重的交点。但是当维数变得更高时,两个不同的代数簇之间的相交理论就变得非常的复杂。当我们失去想象之后,微积分在这个问题上也很难帮助我们,而代数却可以给出一些清晰具体的算法,从而帮助我们去计算理解这些问题。
第三点是采用代数的方法后,我们能够将抽象代数中所发展的各项理论都运用到代数几何的研究中。尤其是代数几何和数论的结合所产生的所谓算术几何的学科。大家都知道著名的费马大定理,\(x^{n} + y^{n} = z^{n}\),在 \(n \geq 3\) 时没有非零的整数解。这一问题等价于,\(x^{3} + y^{3} = 1\) 没有有理数解。如果考虑 \(x,y \in \mathbb{R}\),那我们就得到了一条曲线,其中的每个点都是方程的解。但是如果我们考虑有理数 \(\mathbb{Q}\) 上这个方程的解时,问题就变得复杂了。在有理数上,我们无法进行微积分的运算,也就缺少了使用微积分来直接研究这类问题的基础。但是在有理数上,我们有良好定义的加法、减法、乘法、除法(也就是说所有的有理数构成了一个域),因此,我们可以把代数几何的方法运用到这一条“定义在有理数上”的曲线的研究中。而费马大定理的证明正是代数几何与数论相结合后产生的重要成果。
当然,代数几何的范围和研究是非常广泛的,希望我简单的介绍能够帮助对于现代数学不甚了解的人认识究竟什么是代数几何。